Question

13．已知圆Г过点（1，1）、（1，3）、（2，2），P是圆Г的一个动点，若A（-3，4），O为坐标原点，则$\overrightarrow{OP}$•$\overrightarrow{OA}$的最大值为（　　）

• A． 0
• B． 4
• C． 12
• D． 10

Answer 1

分析 先求出圆的标准方程，设P的坐标为（x，y），根据向量的坐标的运算得到$\overrightarrow{OP}$•$\overrightarrow{OA}$=-3x+4y，设-3x+4y=t，即3x-4y+t=0，当直线与圆相切时有最大值．
根据点到直线距离公式即可求出．

解答 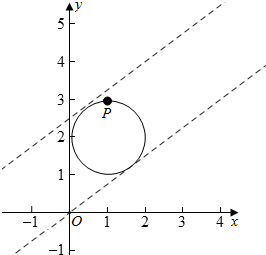解：设圆的标准方程为（x-a）²+（y-b）²=r²，
则$\left\{\begin{array}{l}{（1-a）^{2}+（1-b）^{2}={r}^{2}}\\{（1-a）^{2}+（3-b）^{2}={r}^{2}}\\{（2-a）^{2}+（2-b）^{2}={r}^{2}}\end{array}\right.$，
解得a=1，b=2，r=1，
∴（x-1）²+（y-2）²=1，
设P的坐标为（x，y），
∵A（-3，4），O为坐标原点，
∴$\overrightarrow{OP}$•$\overrightarrow{OA}$=-3x+4y，
设-3x+4y=t，即3x-4y+t=0，
则y=$\frac{3}{4}$x+$\frac{t}{4}$
当直线3x-4y+t=0与圆相切时，t的值最大，
∴d=$\frac{|1×3-2×4+t|}{\sqrt{{3}^{2}+{4}^{2}}}$=1，
即|t-5|=5，
解得t=0，或t=10，
∴t的最大值为10．
∴t的最大值为10．
故选：D．

点评 本题考查了直线和圆的位置关系，圆的方程的解法和向量的坐标运算，属于中档题．