【题目】在正方形
中，边长
，
的中点为
，现将
沿对角线
翻折（如图），则在翻折的过程中.下列说法正确的是______.（填正确命题的序号）
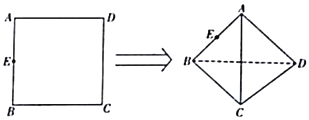
①直线与直线
所成的角为
（
，
不重合时）；
②三棱锥
体积的最大值为
；
③三棱锥
外接球的表面积为
；
④点运动形成的轨迹为椭圆的一部分.
【答案】①③
【解析】
对于①，取
的中点
，连接
，
，得到
，
，
，由线面垂直的判定定理得到
平面
，从而得到
，可判读其正确；对于②，利用三棱锥等体积转换，
，得到当平面
平面
时，体积最大，利用椎体体积公式求得结果，可判读②是错误的；对于③，根据几何体特征，可得的中点为外接球的球心，确定出半径，利用球的表面积公式求得结果，可判读其正确；对于④，点
的轨迹为圆的一部分，从而得到其是错误的，从而得到正确答案.
①取的中点，连接，，∴，，，∴平面，∴，①正确；
②，当平面平面时，三棱锥
的体积最大，此时
，
，②不正确；
③由①的中点为外接球的球心，
，
，③正确；
④点的轨迹为圆的一部分，圆心为上靠近
的4等分点，④不正确；
故答案是：①③.
科目：高中数学 来源： 题型：
【题目】已知函数
的图像过点
和
．
（1）求函数
的解析式；
（2）若
在
上有解，求
的最小值；
（3）记
，
，是否存在正数
，使得
对一切
均成立？若存在，求出的最大值；若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在地上有同样大小的 5 块积木，一堆 2 个，一堆 3 个，要把积木一块一块的全部放到某个盒子里，每次 只能取出其中一堆最上面的一块，则不同的取法有______种（用数字作答）．
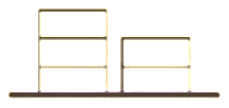
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
（
，
）的图象与
轴交点的横坐标构成一个公差为
的等差数列，把函数
的图象沿轴向左平移
个单位，纵坐标扩大到原来的2倍得到函数
的图象，则下列关于函数的命题中正确的是（ ）
A.函数是奇函数B.的图象关于直线
对称
C.在
上是增函数D.当
时，函数的值域是
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在如图所示的组合体中，三棱柱
的侧面
是圆柱的轴截面，
是圆柱底面圆周上不与
重合的一个点．
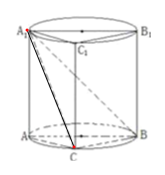
（1）若圆柱的轴截面是正方形，当点是弧
的中点时，求异面直线
与
的所成角的大小；
（2）当点是弧的中点时，求四棱锥
与圆柱的体积比．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了检测某种零件的一条生产线的生产过程，从生产线上随机抽取一批零件，根据其尺寸的数据分成
，
，
，
，
，
，
组，得到如图所示的频率分布直方图.若尺寸落在区间
之外，则认为该零件属“不合格”的零件，其中
，
分别为样本平均和样本标准差，计算可得
（同一组中的数据用该组区间的中点值作代表）.
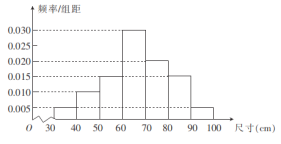
（1）若一个零件的尺寸是
，试判断该零件是否属于“不合格”的零件；
（2）工厂利用分层抽样的方法从样本的前
组中抽出
个零件，标上记号，并从这个零件中再抽取
个，求再次抽取的个零件中恰有
个尺寸小于
的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知椭圆
：
的焦距为2，且过点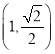
.
（1）求椭圆的方程；
（2）设椭圆的上顶点为
，右焦点为
，直线
与椭圆交于
，
两点，问是否存在直线，使得为
的垂心，若存在，求出直线的方程：若不存在，说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
