
���� ������f��x����1����$lo{g}_{\frac{1}{2}}��2x-1����lo{g}_{\frac{1}{2}}\frac{1}{2}��\left\{\begin{array}{l}2x-1��\frac{1}{2}\\ 2x-1��0\end{array}\right.$����ô𰸣�
����������ʹf��x��������[$\frac{1}{2}$��3]������������aֵ���ۺ����۽���ɵô𰸣�
�����ݺ���f��x��=${log_{\sqrt{66}}}��4{x^2}-x��$Ϊ[$\frac{1}{2}$��3]�ϵ��н��������ϣ����н��ۣ��ɵô𰸣�
��� �⣺����$f��x��={log_{\frac{1}{2}}}��2x-1����1?{log_{\frac{1}{2}}}��2x-1����{log_{\frac{1}{2}}}\frac{1}{2}?\left\{\begin{array}{l}2x-1��\frac{1}{2}\\ 2x-1��0\end{array}\right.$����3�֣�
���$\frac{1}{2}��x��\frac{3}{4}$����4�֣�
����a��1ʱ��$\left\{\begin{array}{l}\frac{1}{2a}��\frac{1}{2}\\ g��\frac{1}{2}��=\frac{1}{4}a-\frac{1}{2}��0\end{array}\right.⇒a��2$����6�֣�
��0��a��1ʱ��$\left\{\begin{array}{l}\frac{1}{2a}��3\\ g��3��=9a-3��0\end{array}\right.⇒\left\{\begin{array}{l}a��\frac{1}{6}\\ a��\frac{1}{3}\end{array}\right.$���⡭��7�֣�
��������a��2����8�֣�
������f��x��=${log_{\sqrt{66}}}��4{x^2}-x��$Ϊ[$\frac{1}{2}$��3]�ϵ��н����������9�֣�
�ɣ�2��֪��$a=\sqrt{66}$ʱ������f��x��Ϊ[$\frac{1}{2}$��3]�ϵĵ�������������
�Ҷ����⻮��T��$\frac{1}{2}={x_0}��{x_1}������{x_{i-1}}��{x_i}������{x_n}=3$��
��$f��\frac{1}{2}��=f��{x_0}����f��{x_1}��������f��{x_{n-1}}����f��{x_n}��=f��3��$��
����f��x1��-f��x0��+f��x2��-f��x1��+��+f��xn��-f��xn-1��=$f��{x_n}��-f��{x_0}��=f��3��-f��\frac{1}{2}��={log_{\sqrt{66}}}33-{log_{\sqrt{66}}}\frac{1}{2}=2$������11�֣�
���Դ��ڳ���M��2��ʹ��$\sum_{i=1}^n{|{f��{x_i}��-f��{x_{i-1}}��}|}��M$�������
����M����СֵΪ2������12�֣�
���� ���⿼���֪ʶ���Ƕ���������ͼ������ʣ��������ն���������ͼ������ʣ��ǽ��Ĺؼ���


 ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -6 | B�� | $\frac{3}{2}$ | C�� | 6 | D�� | $\frac{13}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1} | B�� | {2} | C�� | {0��1} | D�� | {1��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�0] | B�� | [0��+�ޣ� | C�� | ��0��+�ޣ� | D�� | ��-�ޣ�+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 120�� | B�� | 48�� | C�� | 36�� | D�� | 18�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{{\sqrt{6}}}{3}$ | C�� | $\frac{{\sqrt{5}}}{3}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��һ�����ǰ�ABC��ABD�ڳ���ͼ��ʾ��ֱ�����D-AB-C��������BD=2AD��BC=AC��������ֱ��DC��AB���ɽǵ�����ֵΪ��������
��һ�����ǰ�ABC��ABD�ڳ���ͼ��ʾ��ֱ�����D-AB-C��������BD=2AD��BC=AC��������ֱ��DC��AB���ɽǵ�����ֵΪ��������| A�� | $\sqrt{3}$ | B�� | $\sqrt{7}$ | C�� | $\frac{{\sqrt{21}}}{7}$ | D�� | $\frac{{\sqrt{21}}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
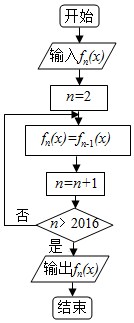 ��ͼ�����ͼ�У���n��N*��n��1��ʱ������fn��x����ʾ����fn-1��x���ĵ���������fn��x��=f��n-1��x���������뺯��f1��x��=sinx+cosx��������ĺ���fn��x��Ϊ��������
��ͼ�����ͼ�У���n��N*��n��1��ʱ������fn��x����ʾ����fn-1��x���ĵ���������fn��x��=f��n-1��x���������뺯��f1��x��=sinx+cosx��������ĺ���fn��x��Ϊ��������| A�� | $\sqrt{2}sin��x+\frac{��}{4}��$ | B�� | $-\sqrt{2}sin��x+\frac{��}{4}��$ | C�� | $\sqrt{2}sin��x-\frac{��}{4}��$ | D�� | $-\sqrt{2}sin��x-\frac{��}{4}��$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com