
【题目】已知函数![]() .
.
(1)当![]() 时,
时,
①若曲线![]() 与直线
与直线![]() 相切,求
相切,求![]() 的值;
的值;
②若曲线![]() 与直线
与直线![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
(2)当![]() 时,不等式
时,不等式![]() 对于任意正实数
对于任意正实数![]() 恒成立,当
恒成立,当![]() 取得最大值时,求
取得最大值时,求![]() 的值.
的值.
【答案】(1)①1 ,②![]() ;(2)1,-1.
;(2)1,-1.
【解析】
![]() 当
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
① 设切点为![]() ,列出方程组,即可求得
,列出方程组,即可求得![]() ,得到答案
,得到答案
②由题意,得方程![]() 有正实数根,即方程
有正实数根,即方程![]() 有正实数根,记
有正实数根,记![]() ,利用导数求得函数的单调性和最小值,即可求解
,利用导数求得函数的单调性和最小值,即可求解![]() 的取值范围
的取值范围
![]() 由题意得,当
由题意得,当![]() 时,
时,![]() 对于任意正实数
对于任意正实数![]() 恒成立,所以当
恒成立,所以当![]() 时,
时,![]() 对于任意正实数
对于任意正实数![]() 恒成立,由
恒成立,由![]() 知,
知,![]() ,进而得到
,进而得到![]() ,
,
![]() ,
,![]() ,……,得到当
,……,得到当![]() 时,
时,![]() ,进而得到
,进而得到![]() 对于任意正实数
对于任意正实数![]() 恒成立,再利用二次函数的性质,即可得到结论
恒成立,再利用二次函数的性质,即可得到结论
(1)解:当![]() 时,
时,![]() ,所以
,所以![]() .
.
①设切点为![]() ,则
,则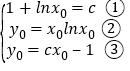
由②③得,![]()
由①得![]() 代入④得,
代入④得,![]()
所以![]() .
.
②由题意,得方程![]() 有正实数根,
有正实数根,
即方程![]() 有正实数根,
有正实数根,
记![]() ,令
,令![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
所以![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数;
上为增函数;
所以![]() .
.
若![]() ,则
,则![]() ,不合;
,不合;
若![]() ,由①知适合;
,由①知适合;
若![]() ,则
,则![]() ,又
,又![]() ,
,
所以![]() ,由零点存在性定理知
,由零点存在性定理知![]() 在
在![]() 上必有零点.
上必有零点.
综上,c的取值范围为![]() .
.
(2)由题意得,当![]() 时,
时,![]() 对于任意正实数x恒成立,
对于任意正实数x恒成立,
所以当![]() 时,
时,![]() 对于任意正实数x恒成立,
对于任意正实数x恒成立,
由(1)知,![]() ,
,
两边同时乘以x得,![]() ①
①
两边同时加上![]() 得,
得,![]() ②,
②,
所以![]() (*),当且仅当
(*),当且仅当![]() 时取等号.
时取等号.
对(*)式重复以上步骤①②可得,![]() ,
,
进而可得,![]() ,
,![]() ,……,
,……,
所以当![]() ,
,![]() 时,
时,![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
所以![]() .
.
当![]() 取最大值1时,
取最大值1时,![]()
令上式中![]() 得,
得, ![]() ,所以
,所以![]() ,
,
所以![]() 对于任意正实数x恒成立,
对于任意正实数x恒成立,
即![]() 对于任意正实数x恒成立,
对于任意正实数x恒成立,
所以![]() ,所以函数
,所以函数![]() 的对称轴
的对称轴![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() ,
,![]() .
.
又由![]() ,两边同乘以x2得,
,两边同乘以x2得,![]() ,
,
所以当![]() ,
,![]() 时,
时,![]() 也恒成立,
也恒成立,
综上,得![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .
.
(Ⅰ)若![]() ,在折叠后的线段
,在折叠后的线段![]() 上是否存在一点
上是否存在一点![]() ,且
,且![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅱ)当三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现对一块长![]() 米,宽
米,宽![]() 米的矩形场地ABCD进行改造,点E为线段BC的中点,点F在线段CD或AD上(异于A,C),设
米的矩形场地ABCD进行改造,点E为线段BC的中点,点F在线段CD或AD上(异于A,C),设![]() (单位:米),
(单位:米),![]() 的面积记为
的面积记为![]() (单位:平方米),其余部分面积记为
(单位:平方米),其余部分面积记为![]() (单位:平方米).
(单位:平方米).
(1)求函数![]() 的解析式;
的解析式;
(2)设该场地中![]() 部分的改造费用为
部分的改造费用为![]() (单位:万元),其余部分的改造费用为
(单位:万元),其余部分的改造费用为![]() (单位:万元),记总的改造费用为W单位:万元),求W最小值,并求取最小值时x的值.
(单位:万元),记总的改造费用为W单位:万元),求W最小值,并求取最小值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠BAC=90°,AC=AB=AA1,E是BC的中点.

(1)求证:AE⊥B1C;
(2)求异面直线AE与A1C所成的角的大小;
(3)若G为C1C中点,求二面角C-AG-E的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司一年需购买某种原料400吨,设公司每次都购买![]() 吨,每次运费为4万元,一年的总存储费用为
吨,每次运费为4万元,一年的总存储费用为![]() 万元.
万元.
(1)要使一年的总运费与总存储费用之和最小,则每次购买多少吨?
(2)要使一年的总运费与总存储费用之和不超过200万元,则每次购买量在什么范围?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为![]() ,
, ![]() ,…,
,…, ![]() 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
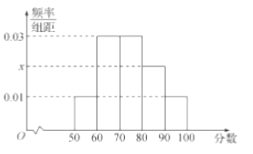
(1)求频率分布直方图中的![]() 的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
(2)若高三年级共有2000名学生,试估计高三学生中这次测试成绩不低于70分的人数;
(3)若在样本中,利用分层抽样的方法从成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求![]() 两组中至少有1人被抽到的概率.
两组中至少有1人被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按照国家质量标准:某种工业产品的质量指标值落在[100,120)内,则为合格品,否则为不合格品.某企业有甲乙两套设备生产这种产品,为了检测这两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本对规定的质量指标值进行检测.表1是甲套设备的样本频数分布表,图1是乙套设备的样本频率分布直方图.

质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 4 | 19 | 20 | 5 | 1 |
表1:甲套设备的样本频数分布表
(1)将频率视为概率,若乙套设备生产了5000件产品,则其中合格品约有多少件?
(2)填写下面2×2列联表,并根据列联表判断是否有95%的把握认为这种产品的质量指标值与甲乙两套设备的选择有关:
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(3)根据表和图,对甲、乙两套设备的优劣进行比较.参考公式及数据:x2=![]()
P(Х2≥k) | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com