
| A. | $({1,\frac{{\sqrt{3}}}{3}})$ | B. | $({0,\frac{{\sqrt{3}}}{3}})$ | C. | $({0,\frac{{2\sqrt{3}}}{3}})$ | D. | $({1,\frac{{2\sqrt{3}}}{3}})$ |
分析 c=2acosB+a,利用正弦定理可得:sinC=2sinAcosB+sinA,又sinC=sin(A+B),代入化为:sin(B-A)=sinA.A,B为锐角,可得:B-A=A,可得:B=2A∈(0,$\frac{π}{2}$),A∈(0,$\frac{π}{4}$),又C=π-3A∈(0,$\frac{π}{2}$),可得:A∈($\frac{π}{6}$,$\frac{π}{3}$),k可得B∈$(\frac{π}{3},\frac{π}{2})$.代入$\frac{{sin({B-A})}}{sinAsinB}$=$\frac{sinA}{sinAsinB}$=$\frac{1}{sinB}$.即可得出.
解答 解:∵c=2acosB+a,∴sinC=2sinAcosB+sinA,即sin(A+B)=2sinAcosB+sinA,
化为:sin(B-A)=sinA.
∵A,B为锐角,可得:B-A=A,可得:B=2A∈(0,$\frac{π}{2}$),
∴A∈(0,$\frac{π}{4}$),
又∵C=π-3A∈(0,$\frac{π}{2}$),可得:A∈($\frac{π}{6}$,$\frac{π}{3}$),∴B∈$(\frac{π}{3},\frac{π}{2})$.
∴$\frac{\sqrt{3}}{2}<$sinB<1.
则$\frac{{sin({B-A})}}{sinAsinB}$=$\frac{sinA}{sinAsinB}$=$\frac{1}{sinB}$.
∴$\frac{{sin({B-A})}}{sinAsinB}$=$\frac{sinA}{sinAsinB}$=$\frac{1}{sinB}$∈$(1,\frac{2\sqrt{3}}{3})$.
故选:D.
点评 本题考查了正弦定理、三角函数的单调性与求值、锐角三角形的性质,考查了推理能力与计算能力,属于中档题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:解答题
| 排除人数 | 0--5 | 6--10 | 11--15 | 16--20 | 21--25 | 25人以上 |
| 概率 | 0.1 | 0.15 | 0.25 | 0.25 | 0.2 | 0.05 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
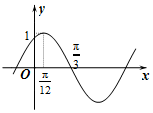 $f(x)=Asin(ωx+φ)(A>0,|φ|<\frac{π}{2})$的图象如图所示,为了得到f(x)的图象,则只要将g(x)=cos2x的图象( )
$f(x)=Asin(ωx+φ)(A>0,|φ|<\frac{π}{2})$的图象如图所示,为了得到f(x)的图象,则只要将g(x)=cos2x的图象( )| A. | 向右平移$\frac{π}{12}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{12}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com