Question

12．下列说法中，正确的有③④．（写出所有正确说法的序号）
①已知关于x的不等式mx²+mx+1＞0的解集为R，则实数m的取值范围是0＜m＜4．
②已知等比数列{a_n}的前n项和为S_n，则S_n、S_2n-S_n、S_3n-S_2n也构成等比数列．
③已知a＞0，b＞-1，且a+b=1，则$\frac{{a}^{2}+2}{a}$+$\frac{{b}^{2}}{b+1}$的最小值为$\frac{3+2\sqrt{2}}{2}$．
④在△DEF中，DE=2，EF=3，∠DEF=60°，M是DF的中点，N在EF上，且DN⊥ME，则$\overrightarrow{DN}$•$\overrightarrow{EF}$=$\frac{9}{4}$．

Answer 1

分析 对m讨论，m=0，m＞0，判别式小于0，m＜0，解不等式即可判断①；
若等比数列{a_n}的前n项和为S_n，若公比q=-1，n为偶数，即可判断②；
将$\frac{{a}^{2}+2}{a}$+$\frac{{b}^{2}}{b+1}$，结合条件，变形为$\frac{2}{a}$+$\frac{1}{b+1}$=$\frac{1}{2}$[a+（b+1）]（$\frac{2}{a}$+$\frac{1}{b+1}$），展开后运用基本不等式，可得最小值，即可判断③；
以E为坐标原点，EF所在直线为x轴，建立直角坐标系，求出D和M的坐标，设N（n，0），由两直线垂直条件：斜率之积为-1，求得n，再由向量的坐标和数量积的坐标表示，计算即可得到所求值，即可判断④．

解答 解：对于①，关于x的不等式mx²+mx+1＞0的解集为R，
当m=0时，不等式即为1＞0，成立；当m＞0，判别式△=m²-4m＜0，解得0＜m＜4；
当m＜0不恒成立．则实数m的取值范围是0≤m＜4．故①错；
对于②，若等比数列{a_n}的前n项和为S_n，若公比q=-1，n为偶数，则S_n、S_2n-S_n、S_3n-S_2n，均为0，
则S_n、S_2n-S_n、S_3n-S_2n不构成等比数列．故②错；
对于③，a＞0，b＞-1，且a+b=1，则$\frac{{a}^{2}+2}{a}$+$\frac{{b}^{2}}{b+1}$=a+$\frac{2}{a}$+$\frac{（b+1）^{2}-2（b+1）+1}{b+1}$
=a+b+1-2+$\frac{2}{a}$+$\frac{1}{b+1}$=$\frac{2}{a}$+$\frac{1}{b+1}$=$\frac{1}{2}$[a+（b+1）]（$\frac{2}{a}$+$\frac{1}{b+1}$）=$\frac{1}{2}$[2+1+$\frac{a}{b+1}$+$\frac{2（b+1）}{a}$]
≥$\frac{1}{2}$[3+2$\sqrt{\frac{a}{b+1}•\frac{2（b+1）}{a}}$]=$\frac{3+2\sqrt{2}}{2}$．当且仅当a=$\sqrt{2}$（b+1）取得等号．
则所求最小值为$\frac{3+2\sqrt{2}}{2}$．故③正确；
对于④，在△DEF中，DE=2，EF=3，∠DEF=60°，
M是DF的中点，N在EF上，建立坐标系如图：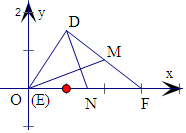
可得D的坐标为（2cos60°，2sin60°），即为（1，$\sqrt{3}$），
又E（0，0），F（3，0），则M（2，$\frac{\sqrt{3}}{2}$），
设N（n，0），由DN⊥ME，可得k_DN•k_ME=-1，
即有$\frac{\sqrt{3}}{1-n}$•$\frac{\sqrt{3}}{4}$=-1，可得n=$\frac{7}{4}$，即有N（$\frac{7}{4}$，0），
则$\overrightarrow{DN}$•$\overrightarrow{EF}$=（$\frac{3}{4}$，-$\sqrt{3}$）•（3，0）=$\frac{3}{4}$×3+（-$\sqrt{3}$）×0=$\frac{9}{4}$．
故④正确．
故答案为：③④．

点评 本题考查命题的真假判断和运用，考查不等式恒成立问题的解法，以及等比数列前n项和的性质，基本不等式的运用和向量数量积的坐标表示，考查化简整理的运算能力，属于中档题．