
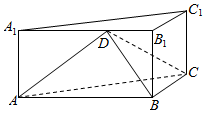
 如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠ABC=90°,AB=2,BC=BB1=1,D是棱A1B1上一点.
如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠ABC=90°,AB=2,BC=BB1=1,D是棱A1B1上一点.分析 (Ⅰ)根据线面垂直的性质定理证明BC⊥平面ABB1A1,即可证明:BC⊥AD;
(Ⅱ)利用转化法结合三棱锥的体积公式即可求三棱锥B-ACD的体积.
解答 证明:(Ⅰ)在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠ABC=90°,
∴BC⊥AB,
∵BB1⊥平面ABC,BC?平面ABC,
∴BB1⊥BC,
∵BB1∩AB=B,
∴BC⊥平面ABB1A1,
∵AD?平面ABB1A1,
∴BC⊥AD.
(Ⅱ)∵BC⊥平面ABB1A1,
∴BC是三棱锥C-ABD的高,
则VB-ACD=VC-ABD=$\frac{1}{3}$S△ABD•BC=$\frac{1}{3}×$$\frac{1}{2}$AB•BB1•BC=$\frac{1}{3}×$$\frac{1}{2}$×2×1=$\frac{1}{3}$,
即${V_{B-ACD}}=\frac{1}{3}$.
点评 本题主要考查空间直线的垂直判断以及三棱锥的体积的计算,利用转化法是解决本题的关键.比较基础.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 是奇函数又是偶函数 | D. | 非奇函数非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | d>3 | B. | $d<\frac{15}{4}$ | C. | $3≤d≤\frac{15}{4}$ | D. | $3<d≤\frac{15}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z的最大值为10,无最小值 | B. | z的最小值为3,无最大值 | ||
| C. | z的最大值为10,最小值为3 | D. | z的最大值为10,最小值为3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,2,4} | B. | {0,1,4} | C. | {0,4} | D. | {1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{9}{8}$ | C. | 1 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com