
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 设复数x=a+bi(a,b∈R),代入方程x2-5|x|+6=0中,利用复数的代数运算求出a、b的值,即得复数x.
解答 解:设x=a+bi(a,b∈R),
代入x2-5|x|+6=0,得(a+bi)2-5$\sqrt{{a}^{2}{+b}^{2}}$+6=0,
即a2-b2+2abi-5$\sqrt{{a}^{2}{+b}^{2}}$+6=0,
∴$\left\{\begin{array}{l}{{a}^{2}{-b}^{2}-5\sqrt{{a}^{2}{+b}^{2}}+6=0①}\\{2ab=0②}\end{array}\right.$,
由②得ab=0,
当a=0时,代入①得:|b|2+5|b|-6=0,解得|b|=1,b=±1,
∴x=±i;
当b=0时,代入①得:|a|2-5|a|+6=0,解得|a|=2或|a|=3,a=±2或a=±3,
∴x=±2或x=±3.
∴复数集内方程x2-5|x|+6=0的解的个数是6.
故选:C.
点评 本题考查了复数代数形式的乘除运算,考查了复数相等的条件,是基础的计算题.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{3}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一定共线 | B. | 一定不共线 | C. | 可能共线 | D. | 可能不共线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
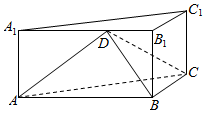 如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠ABC=90°,AB=2,BC=BB1=1,D是棱A1B1上一点.
如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠ABC=90°,AB=2,BC=BB1=1,D是棱A1B1上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{199}{200}$ | B. | $\frac{197}{198}$ | C. | $\frac{197}{199}$ | D. | $\frac{198}{199}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com