
分析 运用切化弦和两角和的正弦公式及诱导公式,再由正弦定理、余弦定理,即可得答案.
解答 解:在△ABC中,$\frac{tanA}{tanB}$+$\frac{tanA}{tanC}$=3,
∴$\frac{sinAcosB}{cosAsinB}+\frac{sinAcosC}{cosAsinC}=3$.
∴$\frac{sinA(cosBsinC+cosCsinB)}{cosAsinBsinC}=3$,即$\frac{sinAsin(C+B)}{cosAsinBsinC}=3$,
∴$\frac{si{n}^{2}A}{cosAsinBsinC}=3$.
根据正弦定理得:$\frac{{a}^{2}}{bccosA}=3$.
∴a2=3bccosA.
又根据余弦定理得:a2=b2+c2-2bccosA,
∴b2+c2-2bccosA=3bccosA.
∴$cosA=\frac{{b}^{2}+{c}^{2}}{5bc}≥\frac{2bc}{5bc}=\frac{2}{5}$.
当且仅当b=c时等号成立,
∴$co{s}^{2}A≥\frac{4}{25}$.
∴$1-si{n}^{2}A≥\frac{4}{25}$,即$si{n}^{2}A≤\frac{21}{25}$,
∴$sinA≤\frac{\sqrt{21}}{5}$.
故答案为:$\frac{\sqrt{21}}{5}$
点评 本题考查三角函数的切化弦,及两角和的正弦公式和诱导公式的运用,同时考查正弦定理和余弦定理的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | y=sin2x | B. | y=cosx | C. | y=sin(2x+$\frac{2π}{3}$) | D. | y=sin(2x-$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
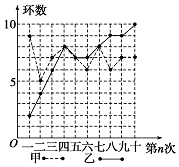 甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:| 平均数 | 方差 | 命中9环及9环以上的次数 | |
| 甲 | |||
| 乙 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2014,+∞) | B. | (0,2014) | C. | (0,2020) | D. | (2020,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+1)2+(y-1)2=2 | B. | (x+1)2+(y-1)2=4 | C. | (x-1)2+(y+1)2=1 | D. | (x-1)2+(y+1)2=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
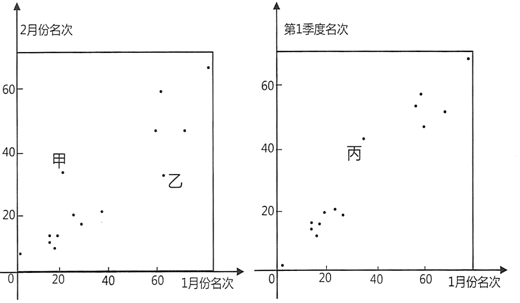
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,4) | C. | (1,4] | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com