[题目]已知函数．(1)若.证明:当时.,当时.,(2)若是的极大值点.求．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知函数．

（1）若，证明：当时，；当时，；

（2）若是的极大值点，求．

【答案】（1）见解析

（2）

【解析】分析：（1）求导，利用函数单调性证明即可。

（2）分类讨论和,构造函数,讨论的性质即可得到a的范围。

详解：（1）当时，，.

设函数，则.

当时，；当时，.故当时，，且仅当时，，从而，且仅当时，.

所以在单调递增.

又，故当时，；当时，.

（2）（i）若，由（1）知，当时，，这与是的极大值点矛盾.

（ii）若，设函数.

由于当时，，故与符号相同.

又，故是的极大值点当且仅当是的极大值点.

如果，则当，且时，，故不是的极大值点.

如果，则存在根，故当，且时，，所以不是的极大值点.

如果，则.则当时，；当时，.所以是的极大值点，从而是的极大值点

综上，.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】等差数列的公差不为0，是其前项和，给出下列命题：

①若，且，则和都是中的最大项；

②给定，对一切，都有；

③若，则中一定有最小项；

④存在，使得和同号.

其中正确命题的个数为（）

A.4B.3C.2D.1

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为提高城市居民生活幸福感，某城市公交公司大力确保公交车的准点率，减少居民乘车候车时间为此，该公司对某站台乘客的候车时间进行统计乘客候车时间受公交车准点率、交通拥堵情况、节假日人流量增大等情况影响在公交车准点率正常、交通拥堵情况正常、非节假日的情况下，乘客候车时间随机变量满足正态分布在公交车准点率正常、交通拥堵情况正常、非节假日的情况下，调查了大量乘客的候车时间，经过统计得到如图频率分布直方图.

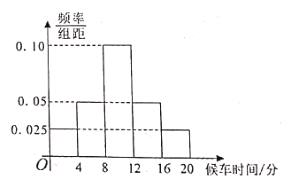
（1）在直方图各组中，以该组区间的中点值代表该组中的各个值，试估计的值；

（2）在统计学中，发生概率低于千分之三的事件叫小概率事件，一般认为，在正常情况下，一次试验中，小概率事件是不能发生的在交通拥堵情况正常、非节假日的某天，随机调查了该站的10名乘客的候车时间，发现其中有3名乘客候车时间超过15分钟，试判断该天公交车准点率是否正常，说明理由.

（参考数据：，，，，）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在正方体ABCD﹣A1B1C1D1中，点E、F、G分别为棱A1D1、A1A、A1B1的中点，给出下列四个命题：①EF⊥B1C；②BC1∥平面EFG；③A1C⊥平面EFG；④异面直线FG、B1C所成角的大小为．其中正确命题的序号为（　　）

A.①②B.②③C.①②③D.①②④

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】武汉某科技公司为提高市场销售业绩，现对某产品在部分营销网点进行试点促销活动．现有两种活动方案，在每个试点网点仅采用一种活动方案，经统计，2018年1月至6月期间，每件产品的生产成本为10元，方案1中每件产品的促销运作成本为5元，方案2中每件产品的促销运作成本为2元，其月利润的变化情况如图①折线图所示．

（1）请根据图①，从两种活动方案中，为该公司选择一种较为有利的活动方案（不必说明理由）；

（2）为制定本年度该产品的销售价格，现统计了8组售价xi（单位：元/件）和相应销量y（单位：件）（i＝1，2，…8）并制作散点图（如图②），观察散点图可知，可用线性回归模型拟合y与x的关系，试求y关于x的回归方程（系数精确到整数）；

参考公式及数据：40，660，xiyi＝206630，x12968，，，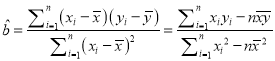

（3）公司策划部选1200lnx+5000和═x3+1200两个模型对销量与售价的关系进行拟合，现得到以下统计值（如表格所示）：

		x3+1200
	52446.95	122.89
	124650
相关指数	R	R

相关指数：R2＝1．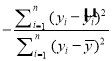

（i）试比较R12，R22的大小（给出结果即可），并由此判断哪个模型的拟合效果更好；

（ii）根据（1）中所选的方案和（i）中所选的回归模型，求该产品的售价x定为多少时，总利润z可以达到最大？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】第7届世界军人运动会于2019年10月18日至27日在湖北武汉举行，赛期10天，共设置射击、游泳、田径、篮球等27个大项，329个小项.共有来自100多个国家的近万名现役军人同台竞技.前期为迎接军运会顺利召开，武汉市很多单位和部门都开展了丰富多彩的宣传和教育活动，努力让大家更多的了解军运会的相关知识，并倡议大家做文明公民.武汉市体育局为了解广大民众对军运会知识的知晓情况，在全市开展了网上问卷调查，民众参与度极高，现从大批参与者中随机抽取200名幸运参与者，他们得分（满分100分）数据，统计结果如下：

组别
频数	5	30	40	50	45	20	10

（1）若此次问卷调查得分整体服从正态分布，用样本来估计总体，设，分别为这200人得分的平均值和标准差（同一组数据用该区间中点值作为代表），求，的值（，的值四舍五入取整数），并计算；

（2）在（1）的条件下，为感谢大家参与这次活动，市体育局还对参加问卷调查的幸运市民制定如下奖励方案：得分低于的可以获得1次抽奖机会，得分不低于的可获得2次抽奖机会，在一次抽奖中，抽中价值为15元的纪念品A的概率为，抽中价值为30元的纪念品B的概率为.现有市民张先生参加了此次问卷调查并成为幸运参与者，记Y为他参加活动获得纪念品的总价值，求Y的分布列和数学期望，并估算此次纪念品所需要的总金额.

（参考数据：；；.）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系中，已知椭圆的左、右顶点分别为.右焦点为，过点且斜率为的直线交椭圆于另一点.

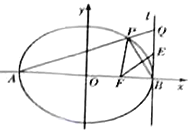
(1)求椭圆的离心率;

(2)若，设直线，延长交直线于点，线段的中点为，求证:点关于直线的对称点在直线上

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】2019举国上下以各种不同的形式共庆新中国成立70周年，某商家计划以“我和我的祖国"为主题举办一次有奖消费活动，此商家先把某品牌酒重新包装，包装时在每瓶酒的包装盒底部随机印上“中"国"“梦”三个字样中的一个，之后随机装箱（1箱4瓶），并规定：若顾客购买的一箱酒中的四瓶酒底部所印的字为同一个字，则此顾客获得一等奖，此箱洒可优惠36元；若顾客购买的一箱酒的四瓶洒底部集齐了“中"“国"二字且仅有此二字，则此顾客获得二等奖，此箱洒可优惠27元；若顾客购买的一箱酒中的四瓶酒的底部集齐了“中”“国"“梦”三个字，则此顾客获得三等奖，此箱酒可优惠18元（注：每箱单独兑奖，箱与箱之间的包装盒不能混）.

（1）①设为顾客购买一箱酒所优惠的钱数，求的分布列；