
【题目】2019举国上下以各种不同的形式共庆新中国成立70周年,某商家计划以“我和我的祖国"为主题举办一次有奖消费活动,此商家先把某品牌酒重新包装,包装时在每瓶酒的包装盒底部随机印上“中"国"“梦”三个字样中的一个,之后随机装箱(1箱4瓶),并规定:若顾客购买的一箱酒中的四瓶酒底部所印的字为同一个字,则此顾客获得一等奖,此箱洒可优惠36元;若顾客购买的一箱酒的四瓶洒底部集齐了“中"“国"二字且仅有此二字,则此顾客获得二等奖,此箱洒可优惠27元;若顾客购买的一箱酒中的四瓶酒的底部集齐了“中”“国"“梦”三个字,则此顾客获得三等奖,此箱酒可优惠18元(注:每箱单独兑奖,箱与箱之间的包装盒不能混).
(1)①设![]() 为顾客购买一箱酒所优惠的钱数,求
为顾客购买一箱酒所优惠的钱数,求![]() 的分布列;
的分布列;
②若不计其他损耗,商家重新包装后每箱酒提价a元,试问a取什么范围时才能使活动后的利润不会小于搞活动之前?
(2)若顾客一次性购买3箱酒,并都中奖,可再加赠一张《我和我的祖国》电影票,顾客小张一次性购买3箱酒,共优惠了72元,试问小张能否得到电影票,概率多大?
【答案】(1)①分布列见解析;②![]() 时,搞活动后的利润不会小于搞活动之前;(2)能,
时,搞活动后的利润不会小于搞活动之前;(2)能,![]() .
.
【解析】
(1)分析题意得到![]() 的所有可能取值后,利用古典概型的概率公式求得概率后可得分布列和期望,根据期望值可得答案;
的所有可能取值后,利用古典概型的概率公式求得概率后可得分布列和期望,根据期望值可得答案;
(2)分析题意得到小张能得到电影票和不能得到电影票的情况后,根据古典概型概率公式可以得到答案.
(1)①![]() 的所有可能取值为36,27,18,0,
的所有可能取值为36,27,18,0,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
则![]() 的分布列为:
的分布列为:
| 36 | 27 | 18 | 0 |
P |
|
|
|
|
②因为![]() .
.
所以当![]() 时,搞活动后的利润不会小于搞活动之前.
时,搞活动后的利润不会小于搞活动之前.
(2)因为![]() ,
,
所以若三箱酒中两箱中一等奖,另一箱不中奖,则小张不能得到电影票;
若三箱酒中两箱中二等奖,另一箱中三等奖,或一箱中一等奖,两箱中三等奖,则小张能得到电影票,概率设为![]() ,
,
则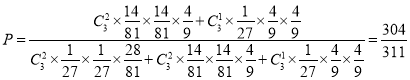 .
.
∴能,得到电影票的概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆C:
中,已知椭圆C:![]() (
(![]() >
>![]() >0)的右焦点为F(1,0),且过点(1,
>0)的右焦点为F(1,0),且过点(1,![]() ),过点F且不与
),过点F且不与![]() 轴重合的直线
轴重合的直线![]() 与椭圆C交于A,B两点,点P在椭圆上,且满足
与椭圆C交于A,B两点,点P在椭圆上,且满足![]() .
.
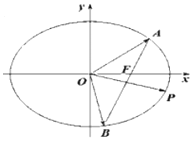
(1)求椭圆C的标准方程;
(2)若![]() ,求直线AB的方程.
,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 经过点
经过点![]() ,且和直线
,且和直线![]() 相切.
相切.
(Ⅰ)求该动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,若斜率为1的直线
,若斜率为1的直线![]() 与线段
与线段![]() 相交(不经过坐标原点
相交(不经过坐标原点![]() 和点
和点![]() ),且与曲线
),且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中a为常数:e≈2.71828为自然对数的底数.
,其中a为常数:e≈2.71828为自然对数的底数.
(1)求曲线y=f(x)在x=0处的切线l在两坐标轴上的截距相等,求a的值;
(2)若x>0,不等式![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如图2).
(如图2).![]() 为
为![]() 中点
中点
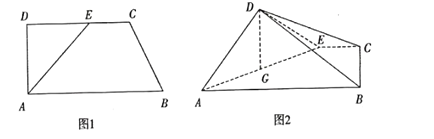
(1)求证:![]() ;
;
(2)求四棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com