
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(3)对任意![]() ,恒有
,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() (2)函数
(2)函数![]() 取得最大值
取得最大值![]() (3)
(3)![]()
【解析】
(1)将![]() 代入函数,去掉绝对值得到分段函数,然后分别求导,利用导数求函数的单调区间.
代入函数,去掉绝对值得到分段函数,然后分别求导,利用导数求函数的单调区间.
(2)![]() ,则
,则![]() ,对函数求导,判断单调性,根据单调性即可得出函数在区间
,对函数求导,判断单调性,根据单调性即可得出函数在区间![]() 上的最大值.
上的最大值.
(3)由(1)(2)得,![]() ,分情况讨论
,分情况讨论![]() 、
、![]() 时函数的单调性,从而得出实数
时函数的单调性,从而得出实数![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时, 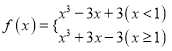 ,
,
若![]() 时,则
时,则![]() ,令
,令![]() ,解得
,解得![]() ;
;
若![]() 时,则
时,则![]() 恒成立,所以
恒成立,所以![]() ,
,
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() .
.
(2)若![]() ,当
,当![]() 时,
时,![]() ,
,![]() .
.
令![]() ,解得
,解得![]() 或
或![]() .
.
列表如下:
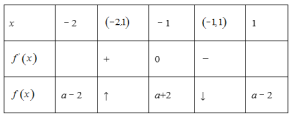
当![]() 时,函数
时,函数![]() 取得最大值
取得最大值![]() .
.
(3)由(1)(2)得,![]() .
.
①当![]() 时,即
时,即![]() 时,
时,
![]() ,即
,即![]() .
.
因为![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时, ![]() 取得最小值
取得最小值![]() ,
,
所以![]() ,解得
,解得![]() ,又
,又![]() ,所以
,所以![]() .
.
②当![]() 即
即![]() 时,
时,
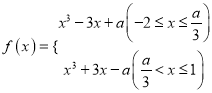
当![]() 时,
时,![]() ,即
,即![]() ,
,
与![]() 矛盾,
矛盾,
所以,实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】2019举国上下以各种不同的形式共庆新中国成立70周年,某商家计划以“我和我的祖国"为主题举办一次有奖消费活动,此商家先把某品牌酒重新包装,包装时在每瓶酒的包装盒底部随机印上“中"国"“梦”三个字样中的一个,之后随机装箱(1箱4瓶),并规定:若顾客购买的一箱酒中的四瓶酒底部所印的字为同一个字,则此顾客获得一等奖,此箱洒可优惠36元;若顾客购买的一箱酒的四瓶洒底部集齐了“中"“国"二字且仅有此二字,则此顾客获得二等奖,此箱洒可优惠27元;若顾客购买的一箱酒中的四瓶酒的底部集齐了“中”“国"“梦”三个字,则此顾客获得三等奖,此箱酒可优惠18元(注:每箱单独兑奖,箱与箱之间的包装盒不能混).
(1)①设![]() 为顾客购买一箱酒所优惠的钱数,求
为顾客购买一箱酒所优惠的钱数,求![]() 的分布列;
的分布列;
②若不计其他损耗,商家重新包装后每箱酒提价a元,试问a取什么范围时才能使活动后的利润不会小于搞活动之前?
(2)若顾客一次性购买3箱酒,并都中奖,可再加赠一张《我和我的祖国》电影票,顾客小张一次性购买3箱酒,共优惠了72元,试问小张能否得到电影票,概率多大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 为圆
为圆![]() 的圆心.
的圆心.
(1)求椭圆的方程;
(2)已知过椭圆右焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,过
两点,过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
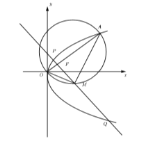
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线上异于原点的任意一点,以
为抛物线上异于原点的任意一点,以![]() 为直径作圆
为直径作圆![]() ,当直线
,当直线![]() 的斜率为1时,
的斜率为1时,![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过焦点![]() 作
作![]() 的垂线
的垂线![]() 与圆
与圆![]() 的一个交点为
的一个交点为![]() ,
,![]() 交抛物线于
交抛物线于![]() ,
,![]() (点
(点![]() 在点
在点![]() ,
,![]() 之间),记
之间),记![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司统计了2010~2018年期间公司年收的增加值![]() (万元)以及相应的年增长率
(万元)以及相应的年增长率![]() ,所得数据如下所示:
,所得数据如下所示:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
增加值 | 1555 | 2100 | 2220 | 2740 | 3135 | 3563 | 4041 | 5494.4 | 6475 |
增长率 |
|
|
|
|
|
|
|
|
|
(1)通过散点图可知,可用线性回归模型拟合2010~2014年![]() 与
与![]() 的关系;
的关系;
①求2010~2014年这5年期间公司年利润的增加值的平均数![]() ;
;
②求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)从哪年开始连续三年公司利润增加值的方差最大?(不需要说明理由)
附:参考公式:回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为
中的斜率和截距的最小二乘估计公式分别为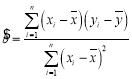 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N个人参加,现将所有参加者按年龄情况分为![]() 等七组,其频率分布直方图如图所示,已知
等七组,其频率分布直方图如图所示,已知![]() 这组的参加者是6人.
这组的参加者是6人.
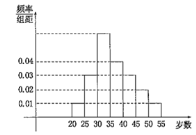
(1)根据此频率分布直方图求N;
(2)组织者从![]() 这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为X,求X的分布列、均值及方差.
这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为X,求X的分布列、均值及方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com