
【题目】已知三棱锥![]() 内接于球O,
内接于球O,![]() 平面ABC,
平面ABC,![]() 为等边三角形,且边长
为等边三角形,且边长![]() ,球
,球![]() 的表面积为
的表面积为![]() ,则直线PC与平面PAB所成的角的正弦值为
,则直线PC与平面PAB所成的角的正弦值为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,点E、F、G分别为棱A1D1、A1A、A1B1的中点,给出下列四个命题:①EF⊥B1C;②BC1∥平面EFG;③A1C⊥平面EFG;④异面直线FG、B1C所成角的大小为![]() .其中正确命题的序号为( )
.其中正确命题的序号为( )
A.①②B.②③C.①②③D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019举国上下以各种不同的形式共庆新中国成立70周年,某商家计划以“我和我的祖国"为主题举办一次有奖消费活动,此商家先把某品牌酒重新包装,包装时在每瓶酒的包装盒底部随机印上“中"国"“梦”三个字样中的一个,之后随机装箱(1箱4瓶),并规定:若顾客购买的一箱酒中的四瓶酒底部所印的字为同一个字,则此顾客获得一等奖,此箱洒可优惠36元;若顾客购买的一箱酒的四瓶洒底部集齐了“中"“国"二字且仅有此二字,则此顾客获得二等奖,此箱洒可优惠27元;若顾客购买的一箱酒中的四瓶酒的底部集齐了“中”“国"“梦”三个字,则此顾客获得三等奖,此箱酒可优惠18元(注:每箱单独兑奖,箱与箱之间的包装盒不能混).
(1)①设![]() 为顾客购买一箱酒所优惠的钱数,求
为顾客购买一箱酒所优惠的钱数,求![]() 的分布列;
的分布列;
②若不计其他损耗,商家重新包装后每箱酒提价a元,试问a取什么范围时才能使活动后的利润不会小于搞活动之前?
(2)若顾客一次性购买3箱酒,并都中奖,可再加赠一张《我和我的祖国》电影票,顾客小张一次性购买3箱酒,共优惠了72元,试问小张能否得到电影票,概率多大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地自2014年至2019年每年年初统计所得的人口数量如下表所示:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人数/千人 | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)根据表中的数据计算2014年至2018年每年该地人口的增长数量,并描述该地人口数量的变化趋势;
(2)研究人员用函数![]() 拟合该地的人口数量,其中
拟合该地的人口数量,其中![]() 的单位是年,2014年初对应时刻
的单位是年,2014年初对应时刻![]() 的单位是干人,设
的单位是干人,设![]() 的反函数为
的反函数为![]() 求
求![]() 的值(精确到0.1),并解释其实际意义.
的值(精确到0.1),并解释其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水污染现状与工业废水排放密切相关,某工厂深人贯彻科学发展观,努力提高污水收集处理水平,其污水处理程序如下:原始污水必先经过A系统处理,处理后的污水(A级水)达到环保标准(简称达标)的概率为p(0<p<1).经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
某厂现有4个标准水量的A级水池,分别取样、检测,多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有样本不达标,则混合样本的化验结果必不达标,若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放
现有以下四种方案:
方案一:逐个化验;
方案二:平均分成两组化验;方案三;三个样本混在一起化验,剩下的一个单独化验;
方案四:四个样本混在一起化验.
化验次数的期望值越小,则方案越"优".
(1)若![]() ,求2个A级水样本混合化验结果不达标的概率;
,求2个A级水样本混合化验结果不达标的概率;
(2)①若![]() ,现有4个A级水样本需要化验,请问:方案一、二、四中哪个最“优"?②若“方案三”比“方案四"更“优”,求p的取值范围.
,现有4个A级水样本需要化验,请问:方案一、二、四中哪个最“优"?②若“方案三”比“方案四"更“优”,求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 为圆
为圆![]() 的圆心.
的圆心.
(1)求椭圆的方程;
(2)已知过椭圆右焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,过
两点,过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
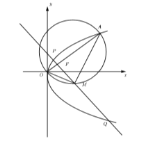
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线上异于原点的任意一点,以
为抛物线上异于原点的任意一点,以![]() 为直径作圆
为直径作圆![]() ,当直线
,当直线![]() 的斜率为1时,
的斜率为1时,![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过焦点![]() 作
作![]() 的垂线
的垂线![]() 与圆
与圆![]() 的一个交点为
的一个交点为![]() ,
,![]() 交抛物线于
交抛物线于![]() ,
,![]() (点
(点![]() 在点
在点![]() ,
,![]() 之间),记
之间),记![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com