
【题目】在正方体ABCD﹣A1B1C1D1中,点E、F、G分别为棱A1D1、A1A、A1B1的中点,给出下列四个命题:①EF⊥B1C;②BC1∥平面EFG;③A1C⊥平面EFG;④异面直线FG、B1C所成角的大小为![]() .其中正确命题的序号为( )
.其中正确命题的序号为( )
A.①②B.②③C.①②③D.①②④
【答案】C
【解析】
画出正方体的直观图,结合线面平行与垂直的判定定理和性质定理逐项判断即可得到正确选项.
如图,
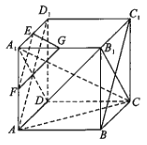
正方体ABCD﹣A1B1C1D1中,A1D//B1C,又A1D⊥EF,故B1C⊥EF,即①正确;
又BC1∥AD1,AD1//EF,故BC1//EF,又EF平面EFG,故BC1∥平面EFG,即②正确;
因为EF⊥A1D,EF⊥A1B1,所以EF⊥平面A1B1CD,又A1C 平面A1B1CD,所以EF⊥A1C,同理可证EG⊥A1C,又EF∩EG=E,EF平面EFG,EG平面EFG,故A1C⊥平面EFG,即③正确;
连接AB1,则AB1//FG,故∠AB1C为异面直线FG与B1C所成角,且∠AB1C=![]() ,即④错误.
,即④错误.
故所有正确命题的序号为①②③.
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx![]() .
.
(1)若a=4,求函数f(x)的单调区间;
(2)若函数f(x)在区间(0,1]内单调递增,求实数a的取值范围;
(3)若x1、x2∈R+,且x1≤x2,求证:(lnx1﹣lnx2)(x1+2x2)≤3(x1﹣x2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆C:
中,已知椭圆C:![]() (
(![]() >
>![]() >0)的右焦点为F(1,0),且过点(1,
>0)的右焦点为F(1,0),且过点(1,![]() ),过点F且不与
),过点F且不与![]() 轴重合的直线
轴重合的直线![]() 与椭圆C交于A,B两点,点P在椭圆上,且满足
与椭圆C交于A,B两点,点P在椭圆上,且满足![]() .
.
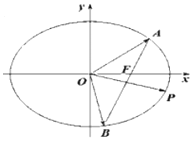
(1)求椭圆C的标准方程;
(2)若![]() ,求直线AB的方程.
,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为a,∠D=60°,点H为DC边中点,现以线段AH为折痕将△DAH折起使得点D到达点P的位置且平面PHA⊥平面ABCH,点E,F分别为AB,AP的中点.

(1)求证:平面PBC∥平面EFH;
(2)若三棱锥P﹣EFH的体积等于![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 经过点
经过点![]() ,且和直线
,且和直线![]() 相切.
相切.
(Ⅰ)求该动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,若斜率为1的直线
,若斜率为1的直线![]() 与线段
与线段![]() 相交(不经过坐标原点
相交(不经过坐标原点![]() 和点
和点![]() ),且与曲线
),且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com