
【题目】设函数![]() ,其中a为常数:e≈2.71828为自然对数的底数.
,其中a为常数:e≈2.71828为自然对数的底数.
(1)求曲线y=f(x)在x=0处的切线l在两坐标轴上的截距相等,求a的值;
(2)若x>0,不等式![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
【答案】(1)a=2(2)a∈(0,1]
【解析】
(1)求导得到 ,求出切线方程为
,求出切线方程为![]() ,利用截距相等得到答案。
,利用截距相等得到答案。
(2)讨论![]() 和
和![]() 两种情况,得到
两种情况,得到![]() ,设函数
,设函数![]() ,讨论
,讨论![]() 和
和![]() 两种情况得到答案。
两种情况得到答案。
(1)f′(x)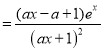 ,f′(0)=1﹣a,f(0)=1,
,f′(0)=1﹣a,f(0)=1,
故切线方程是y=(1﹣a)x+1,由已知得![]() 1,解得:a=2;
1,解得:a=2;
(2)当a<0时,取x0∈(0,![]() ),f(x0)
),f(x0)![]() 0,而
0,而![]() 0与已知矛盾
0与已知矛盾
当a>0时,对x>0,f(x)![]() 即
即![]()
故1![]() 1
1![]() 所以ax+1<ex,
所以ax+1<ex,
设函数g(x)=ex﹣ax﹣1(x>0),则g′(x)=ex﹣a(x>0),
①当0<a≤1时,g′(x)>0恒成立,
故g(x)在(0,+∞)递增,g(x)>g(0)=0,(x>0),
从而不等式ax+1<ex对任意x>0恒成立,于是f(x)![]() 对任意x>0恒成立,
对任意x>0恒成立,
②当a>
故g(lna)<g(0)=0,这与g(x)>0对任意x>0恒成立矛盾,
综上所述:a∈(0,1].


 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:
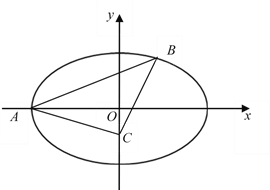
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左顶点为
的左顶点为![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于另一点
交于另一点![]() ,点
,点![]() 为
为![]() 轴上的一点.
轴上的一点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,求直线
为直角顶点的等腰直角三角形,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】武汉某科技公司为提高市场销售业绩,现对某产品在部分营销网点进行试点促销活动.现有两种活动方案,在每个试点网点仅采用一种活动方案,经统计,2018年1月至6月期间,每件产品的生产成本为10元,方案1中每件产品的促销运作成本为5元,方案2中每件产品的促销运作成本为2元,其月利润的变化情况如图①折线图所示.

(1)请根据图①,从两种活动方案中,为该公司选择一种较为有利的活动方案(不必说明理由);
(2)为制定本年度该产品的销售价格,现统计了8组售价xi(单位:元/件)和相应销量y(单位:件)(i=1,2,…8)并制作散点图(如图②),观察散点图可知,可用线性回归模型拟合y与x的关系,试求y关于x的回归方程(系数精确到整数);
参考公式及数据:![]() 40,
40,![]() 660,
660,![]() xiyi=206630,
xiyi=206630,![]() x
x![]() 12968,
12968,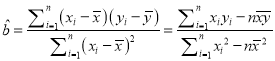 ,
,![]() ,
,
(3)公司策划部选![]() 1200lnx+5000和
1200lnx+5000和![]() ═
═![]() x3+1200两个模型对销量与售价的关系进行拟合,现得到以下统计值(如表格所示):
x3+1200两个模型对销量与售价的关系进行拟合,现得到以下统计值(如表格所示):
|
| |
| 52446.95 | 122.89 |
| 124650 | |
相关指数 | R | R |
相关指数:R2=1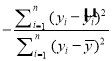 .
.
(i)试比较R12,R22的大小(给出结果即可),并由此判断哪个模型的拟合效果更好;
(ii)根据(1)中所选的方案和(i)中所选的回归模型,求该产品的售价x定为多少时,总利润z可以达到最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
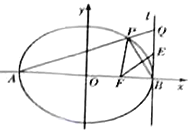
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() .右焦点为
.右焦点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若![]() ,设直线
,设直线![]() ,延长
,延长![]() 交直线
交直线![]() 于点
于点![]() ,线段的
,线段的![]() 中点为
中点为![]() ,求证:点
,求证:点![]() 关于直线
关于直线![]() 的对称点在直线
的对称点在直线![]() 上
上
查看答案和解析>>
科目:高中数学 来源: 题型:
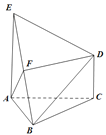
【题目】如图,已知![]() 是正三角形,EA,CD都垂直于平面ABC,且
是正三角形,EA,CD都垂直于平面ABC,且![]() ,二面角
,二面角![]() 的平面角大小为
的平面角大小为![]() ,F是BE的中点,求证:
,F是BE的中点,求证:
(1)![]() 平面ABC;
平面ABC;
(2)![]() 平面EDB;
平面EDB;
(3)求几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019举国上下以各种不同的形式共庆新中国成立70周年,某商家计划以“我和我的祖国"为主题举办一次有奖消费活动,此商家先把某品牌酒重新包装,包装时在每瓶酒的包装盒底部随机印上“中"国"“梦”三个字样中的一个,之后随机装箱(1箱4瓶),并规定:若顾客购买的一箱酒中的四瓶酒底部所印的字为同一个字,则此顾客获得一等奖,此箱洒可优惠36元;若顾客购买的一箱酒的四瓶洒底部集齐了“中"“国"二字且仅有此二字,则此顾客获得二等奖,此箱洒可优惠27元;若顾客购买的一箱酒中的四瓶酒的底部集齐了“中”“国"“梦”三个字,则此顾客获得三等奖,此箱酒可优惠18元(注:每箱单独兑奖,箱与箱之间的包装盒不能混).
(1)①设![]() 为顾客购买一箱酒所优惠的钱数,求
为顾客购买一箱酒所优惠的钱数,求![]() 的分布列;
的分布列;
②若不计其他损耗,商家重新包装后每箱酒提价a元,试问a取什么范围时才能使活动后的利润不会小于搞活动之前?
(2)若顾客一次性购买3箱酒,并都中奖,可再加赠一张《我和我的祖国》电影票,顾客小张一次性购买3箱酒,共优惠了72元,试问小张能否得到电影票,概率多大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com