
甲、乙两篮球运动员进行定点投篮,每人各投4个球,甲投篮命中的概率为 ,乙投篮命中的概率为
,乙投篮命中的概率为 .
.
(1)求甲至多命中2个且乙至少命中2个的概率;
(2)若规定每投篮一次命中得3分,未命中得 分,求乙所得分数
分,求乙所得分数 的概率分布和数学期望.
的概率分布和数学期望.
(1) ;(2)
;(2)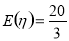
【解析】
试题分析:(1)数学期望是离散型随机变量的一个特征数,它反映了离散型随机变量取值的平均水平,二项分布的期望和方差:若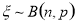 ,则
,则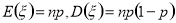 ;(2)求随机变量的分布列的主要步骤:一是明确随机变量的取值,并确定随机变量服从何种概率分布;二是求每一个随机变量取值的概率,三是列成表格;(3)求出分布列后注意运用分布列的两条性质检验所求的分布列是否正确;(4)求解离散随机变量分布列和方差,首先要理解问题的关键,其次要准确无误的找出随机变量的所有可能值,计算出相对应的概率,写成随机变量的分布列,正确运用均值、方差公式进行计算.
;(2)求随机变量的分布列的主要步骤:一是明确随机变量的取值,并确定随机变量服从何种概率分布;二是求每一个随机变量取值的概率,三是列成表格;(3)求出分布列后注意运用分布列的两条性质检验所求的分布列是否正确;(4)求解离散随机变量分布列和方差,首先要理解问题的关键,其次要准确无误的找出随机变量的所有可能值,计算出相对应的概率,写成随机变量的分布列,正确运用均值、方差公式进行计算.
试题解析:【解析】
(1)设“甲至多命中2个球”为事件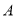 ,“乙至少命中两个球”为事件
,“乙至少命中两个球”为事件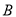 ,由题意得:
,由题意得: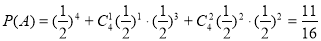 2分
2分
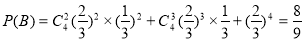 4分
4分
∴甲至多命中2个球且乙至少命中2个球的概率为:
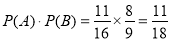 6分
6分
(2)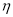 =-4,0,4,8,12,分布列如下:
=-4,0,4,8,12,分布列如下:
η | -4 | 0 | 4 | 8 | 12 |
P |
|
|
|
|
|
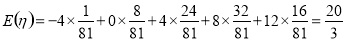 . 12分
. 12分
考点:1、求随机事件的概率;2、离散型随机变量的分布列和数学期望.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| bn+1 |
| bn |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、4025 |
| B、4026 |
| C、22013 |
| D、22014 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n个1 | ||
|
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源:2015届四川省泸州市高三上学期第一次诊断性考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分) 某校校庆,各界校友纷至沓来,某班共来了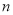 位校友(
位校友(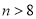 且
且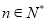 ),其中女校友
),其中女校友 位,组委会对这
位,组委会对这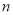 位校友登记制作了一份校友名单,现随机从中选出
位校友登记制作了一份校友名单,现随机从中选出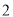 位校友代表,若选出的
位校友代表,若选出的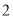 位校友代表是一男一女,则称为“友情搭档”。
位校友代表是一男一女,则称为“友情搭档”。
(1)若随机选出的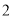 位校友代表为“友情搭档”的概率不小于
位校友代表为“友情搭档”的概率不小于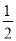 ,求
,求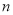 的最大值;
的最大值;
(2)当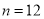 时,设选出的
时,设选出的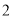 位校友代表中女校友人数为
位校友代表中女校友人数为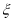 ,求
,求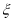 的分布列和均值。
的分布列和均值。
查看答案和解析>>
科目:高中数学 来源:2015届山东省高三第一次诊断性考试文科数学试卷(解析版) 题型:选择题
已知 是三角形
是三角形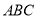 所在平面内一定点,动点
所在平面内一定点,动点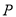 满足
满足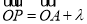 (
( )
)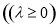 ,则
,则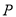 点轨迹一定通过三角形
点轨迹一定通过三角形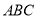 的
的
A.内心 B.外心 C.垂心 D.重心
查看答案和解析>>
科目:高中数学 来源:2015届山东师范大学附属中学高三第一次模拟考试文科数学试卷(解析版) 题型:选择题
设向量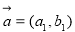 ,
,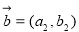 ,定义一种运算“
,定义一种运算“ ”。向量
”。向量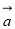

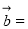
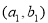

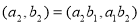 .已知
.已知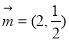 ,
, ,点
,点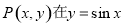 的图象上运动,点Q在
的图象上运动,点Q在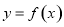 的图象上运动且满足
的图象上运动且满足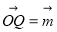

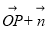 (其中O为坐标原点),则
(其中O为坐标原点),则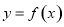 的最小值为( )
的最小值为( )
A.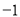 B.
B.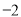 C.2 D.
C.2 D.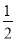
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com