
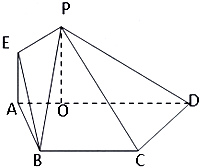
 如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=
如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=| 1 |
| 2 |
| 3 |
| 2 |
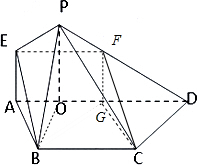 解:(1)作EF∥AD,交PD于F,连结FC,OB,作FG∥EA,交AD于G,连结GC,
解:(1)作EF∥AD,交PD于F,连结FC,OB,作FG∥EA,交AD于G,连结GC,| 1 |
| 2 |
| ∥ |
. |
| ∥ |
. |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2+3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
1+
| ||
| 2 |
| 3 |
5
| ||
| 3 |


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| x |
| A、f(x1)<0,f(x2)<0 |
| B、f(x1)>0,f(x2)<0 |
| C、f(x1)<0,f(x2)>0 |
| D、f(x1)>0,f(x2)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
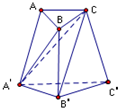 如图所示,三棱台ABC-A′B′C′中,AB:A′B′=1:2,则三棱锥C-A′B′C′,B-A′B′C,A′-ABC的体积之比为( )
如图所示,三棱台ABC-A′B′C′中,AB:A′B′=1:2,则三棱锥C-A′B′C′,B-A′B′C,A′-ABC的体积之比为( )| A、1:1:1 |
| B、2:1:1 |
| C、4:2:1 |
| D、4:4:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
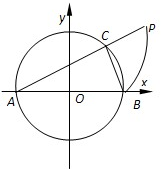 如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )
如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )| A、2π | ||
B、
| ||
| C、π | ||
D、4
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com