
 ���壺���һ�����ε��ĸ��������һ����Բ�ϣ���ô�����ν��������Բ���ڽ����Σ��Ҹ����εĶԽ��ߵĽ���Ϊ�����Բ�����ģ�
���壺���һ�����ε��ĸ��������һ����Բ�ϣ���ô�����ν��������Բ���ڽ����Σ��Ҹ����εĶԽ��ߵĽ���Ϊ�����Բ�����ģ����� ��1����A��x1��y1����B��x2��y2�������������ABCD�ĶԽ�������������ʱ�������������ABCD�ĶԽ��߲�����������ʱ����ֱ��AC�ķ���Ϊ��y=kx����ֱ��BD�ķ���Ϊ��$y=-\frac{1}{k}x$������ֱ�߷��̺���Բ���̣����OA��OB���������������ʽ��ת��Ϊ����k�ĺ��������ɻ�������ʽ����ֵ��
��2����ԭ�㵽������һ�ߵľ���Ϊd����ϣ�1�����õȻ������dΪ��ֵ��˵�����ڶ�Բ��F�е����ζ����У������Բ�ķ��̣�
��3�������ε�һ��AD�ķ���Ϊ$y=t��{x-\sqrt{3}}��$����Ϊһ��ʽ���ɣ�2����ϵ㵽ֱ�ߵľ��빫ʽ���t�ô𰸣�
��� �⣺��1����ͼ����A��x1��y1����B��x2��y2����
�ٵ�����ABCD�ĶԽ�������������ʱ�������Ϊ$4��\frac{1}{2}��2��1=4$��
�ڵ�����ABCD�ĶԽ��߲�����������ʱ����ֱ��AC�ķ���Ϊ��y=kx��
��ֱ��BD�ķ���Ϊ��$y=-\frac{1}{k}x$��
����$\left\{\begin{array}{l}{y=kx}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$����${x_1}^2=\frac{4}{{4{k^2}+1}}$��${y_1}^2=\frac{{4{k^2}}}{{4{k^2}+1}}$��
�Ӷ�$O{A^2}={x_1}^2+{y_1}^2=\frac{{4��{k^2}+1��}}{{4{k^2}+1}}$��
ͬ���ɵã�$O{B^2}={x_2}^2+{y_2}^2=\frac{{4[{{{��{-\frac{1}{k}}��}^2}+1}]}}{{4{{��{-\frac{1}{k}}��}^2}+1}}=\frac{{4��{k^2}+1��}}{{{k^2}+4}}$��
������ABCD�����Ϊ2��OA��OB=$8\sqrt{\frac{{{k^4}+2{k^2}+1}}{{4{k^4}+17{k^2}+4}}}$=$4\sqrt{\frac{{{k^4}+2{k^2}+1}}{{{k^4}+\frac{17}{4}{k^2}+1}}}$
=$4\sqrt{1-\frac{{\frac{9}{4}{k^2}}}{{{k^4}+\frac{17}{4}{k^2}+1}}}$=$4\sqrt{1-\frac{9}{{4��{{k^2}+\frac{1}{k^2}}��+17}}}$$��4\sqrt{1-\frac{9}{{4��2\sqrt{{k^2}��\frac{1}{k^2}}+17}}}$=$\frac{16}{5}$��
�����ҽ���k=��1ʱ�Ⱥų�������
���ϵã�����ABCD����С���Ϊ$\frac{16}{5}$��
��2�����ڶ�Բ${x^2}+{y^2}=\frac{4}{5}$��F�����εĶ����У�
��ԭ�㵽������һ�ߵľ���Ϊd������֤����$d=\frac{2}{{\sqrt{5}}}$��
֤�����ɣ�1��֪��������ABCD�ĶԽ�������������ʱ��$d=\frac{2}{{\sqrt{5}}}$��
������ABCD�ĶԽ��߲�����������ʱ��
${d^2}=\frac{{O{A^2}��O{B^2}}}{{O{A^2}+O{B^2}}}$=$\frac{{\frac{{4��{k^2}+1��}}{{4{k^2}+1}}��\frac{{4��{k^2}+1��}}{{{k^2}+4}}}}{{\frac{{4��{k^2}+1��}}{{4{k^2}+1}}+\frac{{4��{k^2}+1��}}{{{k^2}+4}}}}$=$\frac{{4{{��{k^2}+1��}^2}}}{{��{k^2}+1����{k^2}+4��+��{k^2}+1����4{k^2}+1��}}$
=$\frac{{4{{��{k^2}+1��}^2}}}{{��{k^2}+1����5{k^2}+5��}}=\frac{4}{5}$������$d=\frac{2}{{\sqrt{5}}}$��
���ϣ����ڶ�Բ${x^2}+{y^2}=\frac{4}{5}$��F�е����ζ����У�
��3����ֱ��AD�ķ���Ϊ$y=t��{x-\sqrt{3}}��$����$tx-y-\sqrt{3}t=0$��
���O��0��0����ֱ��AD�ľ���Ϊ$\frac{{|{\sqrt{3}t}|}}{{\sqrt{{t^2}+1}}}=\frac{2}{{\sqrt{5}}}$��
���$t=��\frac{{2\sqrt{11}}}{11}$��
ֱ��AD�ķ���Ϊ$y=��\frac{{2\sqrt{11}}}{11}��{x-\sqrt{3}}��$��
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ���⡢��������ʽ�����ʣ��������������������������ѵ���˴������������ⷽ�����������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-$\frac{��}{4}$��0�� | B�� | ��0��0�� | C�� | ��$\frac{��}{4}$��0�� | D�� | ��$\frac{��}{6}$��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ���� | C�� | �ཻ | D�� | ��m�ı仯���仯 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ֱ�������� | B�� | ֱ�������� | ||
| C�� | ���������� | D�� | ������ֱ�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
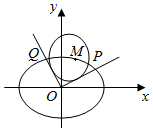 ��֪��ԲC��$\frac{{x}^{2}}{4}$+y2=1����M��x0��y0������ԲC�ϵ�һ�㣬ԲM��x-x0��2+��y-y0��2=r2��
��֪��ԲC��$\frac{{x}^{2}}{4}$+y2=1����M��x0��y0������ԲC�ϵ�һ�㣬ԲM��x-x0��2+��y-y0��2=r2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0���� | B�� | ��0����] | C�� | ��0��4�� | D�� | ��0��4��] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com