
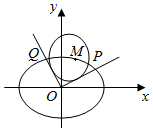
 已知椭圆C:$\frac{{x}^{2}}{4}$+y2=1,点M(x0,y0)是椭圆C上的一点,圆M(x-x0)2+(y-y0)2=r2.
已知椭圆C:$\frac{{x}^{2}}{4}$+y2=1,点M(x0,y0)是椭圆C上的一点,圆M(x-x0)2+(y-y0)2=r2.分析 (1)先求出圆心M($\sqrt{3}$,±$\frac{1}{2}$),由此能求出圆M的方程;
(2)①推导出k1,k2是方程(4-5x02)k2+10x0y0k+4-5y02=0的两根,由此能利用韦达定理能求出k1k2为定值;
②设P(x1,y1),Q(x2,y2),联立$\left\{\begin{array}{l}{y={k}_{1}x}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,由此利用椭圆性质,结合已知条件运用基本不等式能求出|OP|•|OQ|的最大值.
解答 解:(1)椭圆C:$\frac{{x}^{2}}{4}$+y2=1的a=2,b=1,c=$\sqrt{3}$,可得右焦点的坐标为($\sqrt{3}$,0),
即有圆心M($\sqrt{3}$,±$\frac{1}{2}$),
可得圆M的方程为(x-$\sqrt{3}$)2+(y±$\frac{1}{2}$)2=$\frac{1}{4}$;
(2)①k1k2为定值-$\frac{1}{4}$.
由圆M与直线OP:y=k1x相切,
可得$\frac{|k{x}_{0}-{y}_{0}|}{\sqrt{1+{{k}_{1}}^{2}}}$=$\frac{2\sqrt{5}}{5}$,
即(4-5x02)k12+10x0y0k1+4-5y02=0,
同理,(4-5x02)k22+10x0y0k2+4-5y02=0,
即有k1,k2是方程(4-5x02)k2+10x0y0k+4-5y02=0的两根,
可得k1k2=$\frac{4-5{{y}_{0}}^{2}}{4-5{{x}_{0}}^{2}}$=$\frac{4-5(1-\frac{1}{4}{{x}_{0}}^{2})}{4-5{{x}_{0}}^{2}}$=$\frac{-1+\frac{5}{4}{{x}_{0}}^{2}}{4-5{{x}_{0}}^{2}}$=-$\frac{1}{4}$.
②设P(x1,y1),Q(x2,y2),联立$\left\{\begin{array}{l}{y={k}_{1}x}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,
解得x12=$\frac{4}{1+4{{k}_{1}}^{2}}$,y12=$\frac{4{{k}_{1}}^{2}}{1+4{{k}_{1}}^{2}}$,
同理,x22=$\frac{4}{1+4{{k}_{2}}^{2}}$,y22=$\frac{4{{k}_{2}}^{2}}{1+4{{k}_{2}}^{2}}$,
(|OP|•|OQ|)2=($\frac{4}{1+4{{k}_{1}}^{2}}$+$\frac{4{{k}_{1}}^{2}}{1+4{{k}_{1}}^{2}}$)•($\frac{4}{1+4{{k}_{2}}^{2}}$+$\frac{4{{k}_{2}}^{2}}{1+4{{k}_{2}}^{2}}$)
=$\frac{4(1+{{k}_{1}}^{2})}{1+4{{k}_{1}}^{2}}$•$\frac{4(1+{{k}_{2}}^{2})}{1+4{{k}_{2}}^{2}}$=$\frac{4+4{{k}_{1}}^{2}}{1+4{{k}_{1}}^{2}}$•$\frac{1+16{{k}_{1}}^{2}}{1+4{{k}_{1}}^{2}}$≤$\frac{(\frac{5+20{{k}_{1}}^{2}}{2})^{2}}{(1+4{{k}_{1}}^{2})^{2}}$=$\frac{25}{4}$,
当且仅当k1=±$\frac{1}{2}$时,取等号,
可得|OP|•|OQ|的最大值为$\frac{5}{2}$.
点评 本题考查圆的方程的求法,考查两直线的斜率之积是否为定值的判断与求法,考查两线段的最大值的求法,是中档题,解题时要认真审题,注意椭圆性质、韦达定理、圆的性质的合理运用.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:解答题
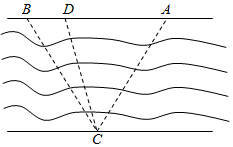 如图,江的两岸可近似的看成两平行的直线,江岸的一侧有A,B两个蔬菜基地,江的另一侧点C处有一个超市.已知A、B、C中任意两点间的距离为20千米.超市欲在AB之间建一个运输中转站D,A,B两处的蔬菜运抵D处后,再统一经过货轮运抵C处.由于A,B两处蔬菜的差异,这两处的运输费用也不同.如果从A处出发的运输费为每千米2元,从B处出发的运输费为每千米1元,货轮的运输费为每千米3元.
如图,江的两岸可近似的看成两平行的直线,江岸的一侧有A,B两个蔬菜基地,江的另一侧点C处有一个超市.已知A、B、C中任意两点间的距离为20千米.超市欲在AB之间建一个运输中转站D,A,B两处的蔬菜运抵D处后,再统一经过货轮运抵C处.由于A,B两处蔬菜的差异,这两处的运输费用也不同.如果从A处出发的运输费为每千米2元,从B处出发的运输费为每千米1元,货轮的运输费为每千米3元. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 定义:如果一个菱形的四个顶点均在一个椭圆上,那么该菱形叫做这个椭圆的内接菱形,且该菱形的对角线的交点为这个椭圆的中心.
定义:如果一个菱形的四个顶点均在一个椭圆上,那么该菱形叫做这个椭圆的内接菱形,且该菱形的对角线的交点为这个椭圆的中心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $6\sqrt{2}$ | B. | 35 | C. | $4\sqrt{3}$ | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1项 | B. | 2k-1项 | C. | 2k项 | D. | 2k+1项 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
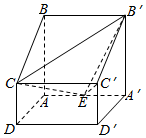 如图,四棱柱ABCD-A′B′C′D′中,侧棱AA′⊥ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA′=AB=2,E为棱AA′的中点.
如图,四棱柱ABCD-A′B′C′D′中,侧棱AA′⊥ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA′=AB=2,E为棱AA′的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com