
分析 (I)直线l的方程为:y=x-c,点(0,b)到l的距离为$\sqrt{2}$,可得$\frac{|0-b-c|}{\sqrt{2}}$=$\sqrt{2}$,即b+c=2,又e=$\frac{\sqrt{2}}{2}$=$\frac{c}{a}$,a2=b2+c2.联立解出即可得出.
(II)F(1,0),可设直线l的方程为:y=k(x-1),E(0,-k),A(x1,y1),B(x2,y2),与椭圆方程联立化为:(1+2k2)x2-4k2x+2k2-2=0,
利用根与系数的关系、数量积运算性质及其$\overrightarrow{MA}$•$\overrightarrow{MB}$=$\overrightarrow{MF}$•$\overrightarrow{ME}$,可得:t=$\frac{2+2{k}^{4}}{1-2{k}^{2}}$,令2k2-1=m∈(-1,0)∪(0,+∞),则t=$\frac{1}{2}(\frac{5}{m}+m+2)$=f(m),利用导数研究其单调性极值与最值即可得出.
解答 解:(I)直线l的方程为:y=x-c,点(0,b)到l的距离为$\sqrt{2}$,∴$\frac{|0-b-c|}{\sqrt{2}}$=$\sqrt{2}$,化为b+c=2,
又e=$\frac{\sqrt{2}}{2}$=$\frac{c}{a}$,a2=b2+c2.联立解得:b=c=1,a2=2.
∴椭圆C的标准方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1.
(II)F(1,0),可设直线l的方程为:y=k(x-1),E(0,-k),A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{y=k(x-1)}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$,化为:(1+2k2)x2-4k2x+2k2-2=0,
∴x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$,
∵$\overrightarrow{MA}$•$\overrightarrow{MB}$=$\overrightarrow{MF}$•$\overrightarrow{ME}$,
∴(x1-t,y1)•(x2-t,y2)=(1-t,0)•(-t,-k),
化为:x1x2-t(x1+x2)+t2+y1y2=t2-t,
∴x1x2-t(x1+x2)+k2x1x2-k2(x1+x2)+k2=-t,
即(1+k2)x1x2-(t+k2)(x1+x2)+t=0,
∴(1+k2)$\frac{2{k}^{2}-2}{1+2{k}^{2}}$-(t+k2)×$\frac{4{k}^{2}}{1+2{k}^{2}}$+t=0,k2≠$\frac{1}{2}$.
化为:t=$\frac{2+2{k}^{4}}{1-2{k}^{2}}$,
令2k2-1=m∈(-1,0)∪(0,+∞),则t=$\frac{2+\frac{1}{2}(1+m)^{2}}{m}$=$\frac{1}{2}(\frac{5}{m}+m+2)$=f(m),
f′(m)=$\frac{1}{2}(1-\frac{5}{{m}^{2}})$=$\frac{(m+\sqrt{5})(m-\sqrt{5})}{2{m}^{2}}$,
∴f(m)分别在m∈(-1,0),m∈(0,$\sqrt{5}$)单调递减;在$(\sqrt{5},+∞)$上单调递增.
∴f(m)∈(-∞,-1)∪$[\sqrt{5}+1,+∞)$.
∴实数t的取值范围是(-∞,-1)∪$[\sqrt{5}+1,+∞)$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、数量积运算性质、利用导数研究其单调性极值与最值,考查了推理能力与计算能力,属于难题.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线x=$\frac{5}{12}$π是函数f(x)的图象的一条对称轴 | |
| B. | 函数f(x)在[0,$\frac{π}{6}$]上单调递减 | |
| C. | 函数f(x)的图象向右平移$\frac{π}{6}$个单位可得到y=cos2x的图象 | |
| D. | 函数f(x)在[0,$\frac{π}{2}$]上的最小值为-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
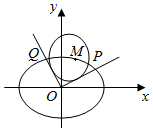 已知椭圆C:$\frac{{x}^{2}}{4}$+y2=1,点M(x0,y0)是椭圆C上的一点,圆M(x-x0)2+(y-y0)2=r2.
已知椭圆C:$\frac{{x}^{2}}{4}$+y2=1,点M(x0,y0)是椭圆C上的一点,圆M(x-x0)2+(y-y0)2=r2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{2}$+y2=1 | B. | $\frac{x^2}{3}$+$\frac{y^2}{2}$=1 | C. | $\frac{x^2}{4}$+y2=1 | D. | $\frac{x^2}{4}$+$\frac{y^2}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),其离心率与双曲线$\frac{x^2}{3}-{y^2}$=1的离心率互为倒数,而直线x+y=$\sqrt{3}$过椭圆C的一个焦点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),其离心率与双曲线$\frac{x^2}{3}-{y^2}$=1的离心率互为倒数,而直线x+y=$\sqrt{3}$过椭圆C的一个焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com