
| A. | (-$\frac{π}{4}$,0) | B. | (0,0) | C. | ($\frac{π}{4}$,0) | D. | ($\frac{π}{6}$,0) |
分析 由sin2(x+θ)=sin[(2x+θ)+θ],展开两角和的正弦,进一步利用两角差的正弦化简得f(x)=-sin2x,由2x=kπ求得x的值得答案.
解答 解:f(x)=2cos(2x+θ)sinθ-sin2(x+θ)
=2cos(2x+θ)sinθ-sin[(2x+θ)+θ]
=2cos(2x+θ)sinθ-sin(2x+θ)cosθ-cos(2x+θ)sinθ
=cos(2x+θ)sinθ-sin(2x+θ)cosθ=-sin2x.
由2x=kπ,得x=$\frac{kπ}{2}$,k∈Z.
∴f(x)图象的一个对称中心的坐标为(0,0).
故选:B.
点评 本题考查三角函数值的恒等变换应用,考查了正弦型函数的图象和性质,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
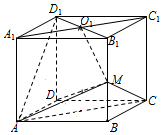 如图,直四棱柱ABCD-A1B1C1D1的棱长均为2,∠BAD=60°,M为BB1的中点,Ol为上底面对角线的交点.
如图,直四棱柱ABCD-A1B1C1D1的棱长均为2,∠BAD=60°,M为BB1的中点,Ol为上底面对角线的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 定义:如果一个菱形的四个顶点均在一个椭圆上,那么该菱形叫做这个椭圆的内接菱形,且该菱形的对角线的交点为这个椭圆的中心.
定义:如果一个菱形的四个顶点均在一个椭圆上,那么该菱形叫做这个椭圆的内接菱形,且该菱形的对角线的交点为这个椭圆的中心.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{1}{2}$个单位长度 | B. | 向右平移$\frac{1}{2}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com