
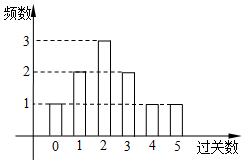
 某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.分析 (Ⅰ)列出小明的过关数与奖品数对应表,由此能求出小明在这十次游戏中所得奖品数的均值.
(Ⅱ)利用等可能事件概率计算公式能求出小明一次游戏后能玩另一个游戏的概率.
(Ⅲ)小明在四次游戏中所得奖品数为{2,2,4,8},小聪在四次游戏中所得奖品数为{4,4,8,16},由此利用列举法能求出小明和小聪所得奖品总数超过10的概率.
解答 解:(Ⅰ)小明的过关数与奖品数如下表:
| 过关数 | 0 | 1 | 2 | 3 | 4 | 5 |
| 奖品数 | 0 | 1 | 2 | 4 | 8 | 16 |
| 2 | 2 | 4 | 8 | |
| 4 | 6 | 6 | 8 | 12 |
| 4 | 6 | 6 | 8 | 12 |
| 8 | 10 | 10 | 12 | 16 |
| 16 | 18 | 18 | 20 | 24 |
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | [$\frac{ln3}{3}$,$\frac{1}{e}$) | B. | [$\frac{ln3}{3}$,$\frac{1}{2e}$] | C. | (0,$\frac{1}{e}$) | D. | (0,$\frac{1}{2e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
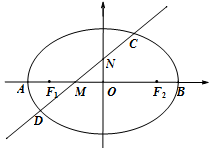 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$或$\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com