
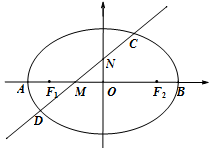
 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.分析 (Ⅰ)由$|{AB}|=4,|{{F_1}{F_2}}|=2\sqrt{3}$,求出$a=2,c=\sqrt{3}$,求出b,得到椭圆方程,然后求解离心率.
(Ⅱ)设C(x1,y1),D(x2,y2)易知$N({0,m}),M({-\frac{m}{k},0})$,由$\left\{{\begin{array}{l}{y=kx+m}\\{{x^2}+4{y^2}=4}\end{array}}\right.$消去y整理,通由△>0韦达定理,设CD的中点为H(x0,y0),求出直线l的垂直平分线方程为$y-\frac{m}{2}=-2({x+m})$,通过过点(-1,0),求解直线l的方程.
解答 解:(Ⅰ)由$|{AB}|=4,|{{F_1}{F_2}}|=2\sqrt{3}$,可知$a=2,c=\sqrt{3}$,可得b=1,
则椭圆方程为$\frac{x^2}{4}+{y^2}=1$….(2分)
离心率是$e=\frac{{\sqrt{3}}}{2}$….(4分)
(Ⅱ)设C(x1,y1),D(x2,y2)易知$N({0,m}),M({-\frac{m}{k},0})$…(5分)
由$\left\{{\begin{array}{l}{y=kx+m}\\{{x^2}+4{y^2}=4}\end{array}}\right.$(k>0)消去y整理得:(1+4k2)x2+8kmx+4m2-4=0
由△>0⇒4k2+m2+1>0,${x_1}+{x_2}=\frac{-8km}{{1+4{k^2}}},{x_1}{x_2}=\frac{{4{m^2}-4}}{{1+4{k^2}}}$…(6分)
且|CM|=|DN|即$\overrightarrow{CM}=\overrightarrow{ND}$可知${x_1}+{x_2}=-\frac{m}{k}$,即$\frac{-8km}{{1+4{k^2}}}=-\frac{m}{k}$,解得$k=\frac{1}{2}$….(8分)${x_1}+{x_2}=-2m,{y_1}+{y_2}=2{m^2}-2$,设CD的中点为H(x0,y0),
则${x_0}=\frac{{{x_1}+{x_2}}}{2}=-m,{y_0}=\frac{{{y_1}+{y_2}}}{2}=\frac{m}{2}$….(10分)
直线l的垂直平分线方程为$y-\frac{m}{2}=-2({x+m})$过点(-1,0),解得$m=\frac{4}{3}$
此时直线l的方程为$y=\frac{1}{2}x+\frac{4}{3}$….(12分)
点评 本题考查椭圆方程的求法,直线与椭圆的位置关系的综合应用,考查计算能力以及转化思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | R | B. | {x|-2≤x≤-1} | C. | {x|-2≤x≤-1或x>2} | D. | {x|-2≤x≤-1或x=2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$+$\frac{5i}{2}$ | B. | -$\frac{1}{2}$-$\frac{5i}{2}$ | C. | $\frac{5}{2}$+$\frac{5i}{2}$ | D. | -$\frac{5}{2}$-$\frac{5i}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
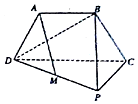 如图,三角形PCD所在的平面与等腰梯形ABCD所在的平面垂直,AB=AD=$\frac{1}{2}$CD,AB∥CD,CP⊥CD,M为PD的中点.
如图,三角形PCD所在的平面与等腰梯形ABCD所在的平面垂直,AB=AD=$\frac{1}{2}$CD,AB∥CD,CP⊥CD,M为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
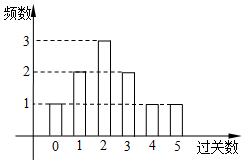 某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com