
分析 根据题意,若$\overrightarrow a⊥\overrightarrow c$,由向量垂直的判定方法可得2x+2×(-6)=0,解可得x的值,即可得$\overrightarrow{a}$的坐标,若$\overrightarrow b∥\overrightarrow c$,由向量平行的坐标表示公式可得2y=1×(-6),解可得y的值,即可得$\overrightarrow{b}$的坐标,由向量加法的坐标计算公式可得$\overrightarrow{a}$+$\overrightarrow{b}$的坐标,由向量模的计算公式计算可得答案.
解答 解:根据题意,向量$\overrightarrow a=({x,2})$,$\overrightarrow b=({1,y})$,$\overrightarrow c=({2,-6})$,
若$\overrightarrow a⊥\overrightarrow c$,则有2x+2×(-6)=0,解可得x=6,即$\overrightarrow{a}$=(6,2),
若$\overrightarrow b∥\overrightarrow c$,则有2y=1×(-6),解可得y=-3,即$\overrightarrow{b}$=(1,-3),
则$\overrightarrow{a}$+$\overrightarrow{b}$=(7,-1),
则$|{\overrightarrow a+\overrightarrow b}|$=$\sqrt{49+1}$=$5\sqrt{2}$;
故答案为:5$\sqrt{2}$.
点评 本题考查向量的数量积的计算,关键是求出$\overrightarrow{a}$、$\overrightarrow{b}$的坐标.


科目:高中数学 来源: 题型:解答题
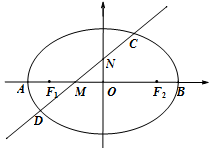 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 1或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 买房 | 不买房 | 纠结 | |
| 城市人 | 5 | 15 | |
| 农村人 | 20 | 10 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com