
| �� | ���� | ���� | |
| ������ | 5 | 15 | |
| ũ���� | 20 | 10 |
| P��k2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
���� ��1����������еIJ�������Ϊx��ũ�����еľ�������Ϊy�����������г���������⼴�ɣ�
��2�������������ϰ������Ա��أ��ɣ�1���õ��������������������������ϰ��ֱ��������������${{K}_{1}}^{2}$��${{K}_{2}}^{2}$��${{K}_{3}}^{2}$���ɱ������ݼ���${{K}_{1}}^{2}$��${{K}_{2}}^{2}$��${{K}_{3}}^{2}$��ֵ�����������ó����ۣ�
��� �⣺��1����������еIJ�������Ϊx��ũ�����еľ�������Ϊy��
��$\left\{\begin{array}{l}{\frac{20+x}{30+y}=\frac{3}{8}}\\{��20+x��+��30+y��=110}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=10}\\{y=50}\end{array}\right.$��
�������г������еIJ�������Ϊ10�ˣ�ũ�����еľ�������Ϊ50�ˣ�
��2�������������ϰ������Ա��أ��ɣ�1���õ����������£�
| �� | ���� | ���� | �ܼ� | |
| ������ | 5 | 10 | 15 | 30 |
| ũ���� | 20 | 10 | 50 | 85 |
| �ܼ� | 25 | 20 | 65 | 110 |
���� ���⿼������ѧģ��������Լ����Ӧ�����⣬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
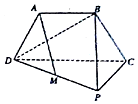 ��ͼ��������PCD���ڵ�ƽ�����������ABCD���ڵ�ƽ�洹ֱ��AB=AD=$\frac{1}{2}$CD��AB��CD��CP��CD��MΪPD���е㣮
��ͼ��������PCD���ڵ�ƽ�����������ABCD���ڵ�ƽ�洹ֱ��AB=AD=$\frac{1}{2}$CD��AB��CD��CP��CD��MΪPD���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | -2 | C�� | 8 | D�� | -8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��һ��ȫ����ѧ�����У�ij��3000������ѧ���ij����ɼ�ͳ����ͼ��ʾ�����ڱ�����ѧ�����У��ɼ���[80��90]�ϵ�ѧ������Ϊ900��
��֪��һ��ȫ����ѧ�����У�ij��3000������ѧ���ij����ɼ�ͳ����ͼ��ʾ�����ڱ�����ѧ�����У��ɼ���[80��90]�ϵ�ѧ������Ϊ900���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 0 | C�� | 2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com