练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知i为虚数单位，复数z满足z（1-i）=3+2i，则z=（　　）
    A．$\frac{1}{2}$+$\frac{5i}{2}$B．-$\frac{1}{2}$-$\frac{5i}{2}$C．$\frac{5}{2}$+$\frac{5i}{2}$D．-$\frac{5}{2}$-$\frac{5i}{2}$

    分析 利用复数的运算法则、共轭复数的定义即可得出．

    解答 解：z（1-i）=3+2i，∴z（1-i）（1+i）=（3+2i）（1+i），∴2z=1+5i，
    则z=$\frac{1}{2}+\frac{5}{2}i$，
    故选：A．

    点评 本题考查了复数的运算法则、共轭复数的定义，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．一儿童游乐场拟建造一个“蛋筒”型游乐设施，其轴截面如图中实线所示．ABCD是等腰梯形，AB=20米，∠CBF=α（F在AB的延长线上，α为锐角）．圆E与AD，BC都相切，且其半径长为100-80sinα米．EO是垂直于AB的一个立柱，则当sinα的值设计为多少时，立柱EO最矮？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．△ABC中，角A、B、C的对边分别为a、b、c，G是平面△ABC上一点，且满足a•$\overrightarrow{GA}$+b•$\overrightarrow{GB}$+c•$\overrightarrow{GC}$=0，则G是△ABC中的（　　）
    A．内心B．外心C．重心D．垂心

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．对于函数f（x）给出定义：设f′（x）是函数f（x）的导函数，f″（x）是函数f′（x）的导函数，若函数f″（x）有零点x0，则称（x0，f（x0））为函数f（x）的“拐点”．某同学经过探究发现：任何一个三次函数f（x）=ax3+bx2+cx+d（a≠0）都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心，给定函数f（x）=$\frac{1}{3}$x3-x2-$\frac{1}{3}$x+2，请你根据上面探究结果，计算$\sum_{i1}^{4035}$f（$\frac{i}{2017}$）=4035．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

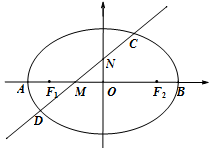    9．如图，椭圆E的左右顶点分别为A、B，左右焦点分别为F1、F2，|AB|=4，|F1F2|=2$\sqrt{3}$，直线l：y=kx+m（k＞0）交椭圆于C、D两点，与线段F1F2及椭圆短轴分别交于M、N两点（M、N不重合），且|CM|=|DN|．
    （Ⅰ）求椭圆E的离心率；
    （Ⅱ）若CD的垂直平分线过点（-1，0），求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．设点O、P、Q是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的渐近线与抛物线y2=4x的交点，O为坐标原点，若△OPQ的面积为2，则双曲线的离心率为$\sqrt{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．设x，y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$，目标函数z=ax+by（a＞0，b＞0）的最大值为M，若M的取值范围是[1，2]，则点M（a，b）所经过的区域面积为（　　）
    A．$\frac{1}{2}$B．$\frac{3}{2}$C．$\frac{5}{2}$D．$\frac{7}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的一条渐近线方程为2x+y=0，则C的离心率为（　　）
    A．$\frac{{\sqrt{5}}}{2}$B．$\frac{{\sqrt{5}}}{2}$或$\sqrt{5}$C．2D．$\sqrt{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知在△ABC中，角A，B，C所对的边分别为a，b，c，若C=2A，c=$\sqrt{3}$a，则$\frac{b}{a}$等于（　　）
    A．1B．2C．$\sqrt{2}$D．1或2

    查看答案和解析>>

    同步练习册答案