
 一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示.ABCD是等腰梯形,AB=20米,∠CBF=α(F在AB的延长线上,α为锐角).圆E与AD,BC都相切,且其半径长为100-80sinα米.EO是垂直于AB的一个立柱,则当sinα的值设计为多少时,立柱EO最矮?
一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示.ABCD是等腰梯形,AB=20米,∠CBF=α(F在AB的延长线上,α为锐角).圆E与AD,BC都相切,且其半径长为100-80sinα米.EO是垂直于AB的一个立柱,则当sinα的值设计为多少时,立柱EO最矮? 分析 以AB所在直线为x轴,以线段AB的垂直平分线为y轴,建立平面直角坐标系,由已知可求直线BC的方程为:xtanα-y-10tanα=0,设圆心E(0,t),(t>0),由圆E与直线BC相切,可求EO=t=$\frac{100-90sinα}{cosα}$,令f(α)=$\frac{100-90sinα}{cosα}$,α∈(0,$\frac{π}{2}$),则f′(α)=$\frac{100(sinα-\frac{9}{10})}{co{s}^{2}α}$,设sinα0=$\frac{9}{10}$,α0∈(0,$\frac{π}{2}$).列表可求EO的最小值.
解答 (本题满分为14分)
解:如图所示,以AB所在直线为x轴,以线段AB的垂直平分线为y轴,建立平面直角坐标系.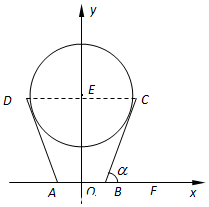
因为B(10,0),kBC=tanα,所以直线BC的方程为:y=tanα(x-10),即xtanα-y-10tanα=0.…(4分)
设圆心E(0,t),(t>0),由圆E与直线BC相切,得100-80sinα=$\frac{|-t-10tanα|}{\sqrt{1+ta{n}^{2}α}}$=$\frac{t+10tanα}{\frac{1}{cosα}}$,
所以EO=t=$\frac{100-90sinα}{cosα}$,…(8分)
令f(α)=$\frac{100-90sinα}{cosα}$,α∈(0,$\frac{π}{2}$),则f′(α)=$\frac{100(sinα-\frac{9}{10})}{co{s}^{2}α}$,…(10分)
设sinα0=$\frac{9}{10}$,α0∈(0,$\frac{π}{2}$).列表如下:
| α | (0,α0) | α0 | (α0,$\frac{π}{2}$) |
| f′(α) | - | 0 | + |
| f(α) | 减 | 极小值 | 增 |
点评 本题主要考查了直线与圆的位置关系,考查了利用导数研究函数的单调性,考查了数形结合思想和转化思想的应用,属于中档题.


科目:高中数学 来源: 题型:填空题
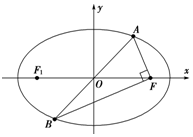 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上有一个点A,它关于原点的对称点为B,点F为椭圆的右焦点,且满足AF⊥BF,当∠ABF=$\frac{π}{12}$时,椭圆的离心率为$\frac{\sqrt{6}}{3}$.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上有一个点A,它关于原点的对称点为B,点F为椭圆的右焦点,且满足AF⊥BF,当∠ABF=$\frac{π}{12}$时,椭圆的离心率为$\frac{\sqrt{6}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 7 | C. | $\frac{5}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | -$\frac{\sqrt{2}}{4}$ | C. | 2$\sqrt{2}$ | D. | -2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$+$\frac{5i}{2}$ | B. | -$\frac{1}{2}$-$\frac{5i}{2}$ | C. | $\frac{5}{2}$+$\frac{5i}{2}$ | D. | -$\frac{5}{2}$-$\frac{5i}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com