
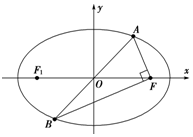
 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上有一个点A,它关于原点的对称点为B,点F为椭圆的右焦点,且满足AF⊥BF,当∠ABF=$\frac{π}{12}$时,椭圆的离心率为$\frac{\sqrt{6}}{3}$.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上有一个点A,它关于原点的对称点为B,点F为椭圆的右焦点,且满足AF⊥BF,当∠ABF=$\frac{π}{12}$时,椭圆的离心率为$\frac{\sqrt{6}}{3}$. 分析 设椭圆的左焦点为F1,连结AF1,BF1,通过|AB|=|F1F|=2c,所以在Rt△ABF中,|AF|=2csin$\frac{π}{12}$,
|BF|=2ccos$\frac{π}{12}$,由椭圆定义,转化求解离心率即可.
解答 解:设椭圆的左焦点为F1,连结AF1,BF1,由对称性及AF⊥BF可知,四边形AFBF1是矩形,所以|AB|=|F1F|=2c,所以在Rt△ABF中,|AF|=2csin$\frac{π}{12}$,
|BF|=2ccos$\frac{π}{12}$,由椭圆定义得:
2c(cos$\frac{π}{12}$+sin$\frac{π}{12}$)=2a,即:
e=$\frac{c}{a}$=$\frac{1}{cos\frac{π}{12}+sin\frac{π}{12}}$=$\frac{1}{\sqrt{2}sin(\frac{π}{4}+\frac{π}{12})}$=$\frac{\sqrt{6}}{3}$.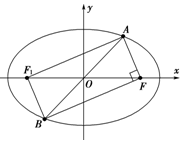
故答案为:$\frac{\sqrt{6}}{3}$.
点评 本题考查椭圆的简单性质的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (0,2] | C. | (1,2) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “x<-2”是“x2+3x+2>0”的必要不充分条件 | |
| B. | 对于命题p:?x0∈R,使得${x_0}^2+{x_0}-1<0$,则¬p:?x∈R,均有x2+x-1≥0 | |
| C. | 命题“若x2-3x+2=0,则x=2”的否命题为若x2-3x+2=0,则x≠2 | |
| D. | 若p∧q为假命题,则p,q均为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{2}{5}+\frac{1}{5}i$ | B. | $\frac{2}{5}-\frac{1}{5}i$ | C. | $\frac{2}{5}+\frac{1}{5}i$ | D. | $-\frac{2}{5}-\frac{1}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+2i | B. | -1+2i | C. | 1-2i | D. | -1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示.ABCD是等腰梯形,AB=20米,∠CBF=α(F在AB的延长线上,α为锐角).圆E与AD,BC都相切,且其半径长为100-80sinα米.EO是垂直于AB的一个立柱,则当sinα的值设计为多少时,立柱EO最矮?
一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示.ABCD是等腰梯形,AB=20米,∠CBF=α(F在AB的延长线上,α为锐角).圆E与AD,BC都相切,且其半径长为100-80sinα米.EO是垂直于AB的一个立柱,则当sinα的值设计为多少时,立柱EO最矮?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com