
| A. | [$\frac{ln3}{3}$,$\frac{1}{e}$) | B. | [$\frac{ln3}{3}$,$\frac{1}{2e}$] | C. | (0,$\frac{1}{e}$) | D. | (0,$\frac{1}{2e}$) |
分析 求出|f(x)|的解析式,作出y=|f(x)|与y=a(x+1)的函数图象,根据交点个数判断a的范围.
解答 解:令g(x)=0得|f(x)|=ax+a=a(x+1),
|f(x)|=$\left\{\begin{array}{l}{2{x}^{2}-3x,-2≤x<0}\\{ln(x+1),0≤x≤2}\end{array}\right.$,
作出y=|f(x)|与y=a(x+1)的函数图象,则两函数图象有3个交点,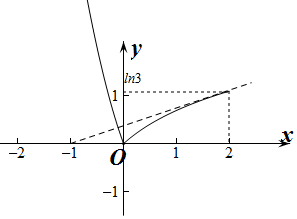
若直线y=a(x+1)经过点(2,ln3),则a=$\frac{ln3}{3}$,
若直线y=a(x+1)与y=ln(x+1)相切,设切点为(x0,y0),
则$\left\{\begin{array}{l}{{y}_{0}=a({x}_{0}+1)}\\{{y}_{0}=ln({x}_{0}+1)}\\{\frac{1}{{x}_{0}+1}=a}\end{array}\right.$,解得x0=e-1,y0=1,a=$\frac{1}{e}$.
∴$\frac{ln3}{3}$≤a<$\frac{1}{e}$,
故选:A.
点评 本题考查来了函数零点与函数图象的关系,导数的几何意义,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | R | B. | {x|-2≤x≤-1} | C. | {x|-2≤x≤-1或x>2} | D. | {x|-2≤x≤-1或x=2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
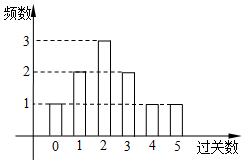 某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com