
对于函数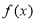 ,若存在区间
,若存在区间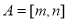 ,使得
,使得 ,则称函数
,则称函数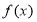 为“和谐函数”,区间
为“和谐函数”,区间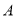 为函数
为函数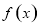 的一个“和谐区间”.给出下列4个函数:
的一个“和谐区间”.给出下列4个函数:
①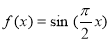 ;②
;②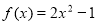 ;③
;③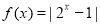 ; ④
; ④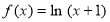 .
.
其中存在唯一“和谐区间”的“和谐函数”为 ( )
A.①②③B.②③④C.①③D.②③
D
【解析】
试题分析:对于①,由于函数 的周期是4,正弦函数的性质我们易得,A=[0,1]为函数的一个“和谐区间”;同时当A=[-1,0]时也是函数的一个“和谐区间”,∴不满足唯一性;
的周期是4,正弦函数的性质我们易得,A=[0,1]为函数的一个“和谐区间”;同时当A=[-1,0]时也是函数的一个“和谐区间”,∴不满足唯一性;
对于②,由于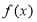 =2x2-1,当A=[-1,1]时,
=2x2-1,当A=[-1,1]时,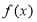 ∈[-1,1],满足条件,且由二次函数的图象可知,满足条件的集合只有A=[-1,1]一个.∴
∈[-1,1],满足条件,且由二次函数的图象可知,满足条件的集合只有A=[-1,1]一个.∴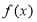 =2x2-1满足题意;
=2x2-1满足题意;
对于③,由指数函数的性质我们易得,M=[0,1]为函数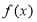 =|2x-1|的“和谐区间”,由指数函数的图象可和,满足条件的集合只有A=[0,1]一个.∴
=|2x-1|的“和谐区间”,由指数函数的图象可和,满足条件的集合只有A=[0,1]一个.∴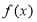 =|2x-1|满足题意;
=|2x-1|满足题意;
对于④,由于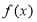 =ln(x+1)单调递增,且函数的定义域为(-1,+∞),若存在“和谐区间”,则满足
=ln(x+1)单调递增,且函数的定义域为(-1,+∞),若存在“和谐区间”,则满足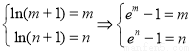 ,∴m,n是方程
,∴m,n是方程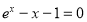 的两个根,设
的两个根,设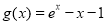 ,
,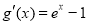 ,当x>0时,
,当x>0时,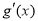 >0,此时函数
>0,此时函数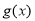 单调递增,当-1<x<0时,
单调递增,当-1<x<0时,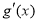 <0,此时函数
<0,此时函数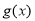 单调递减,且
单调递减,且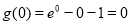 ,故
,故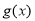 =ex-x-1=0有且只有一个解,故
=ex-x-1=0有且只有一个解,故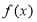 =ln(x+1)不存在“可等域区间”.故存在唯一“和谐区间”的“和谐函数”为:②③.故选:D.
=ln(x+1)不存在“可等域区间”.故存在唯一“和谐区间”的“和谐函数”为:②③.故选:D.
考点:1.函数的概念;2.函数的图象与性质;3.新定义.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:填空题
设函数f(x)=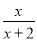 (x>0)
(x>0)
观察:f1(x)=f(x)= ,f2(x)=f(f1(x))=
,f2(x)=f(f1(x))= ,f3(x)=f(f2(x))=
,f3(x)=f(f2(x))= ,
,
f4(x)=f(f3(x))= , 根据以上事实,由归纳推理可得:
, 根据以上事实,由归纳推理可得:
当n∈N*且n≥2时,fn(x)=f(fn-1(x))=________.
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末理科数学试卷(解析版) 题型:解答题
已知曲线C的极坐标方程为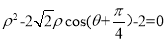 .
.
(1)若直线 过原点,且被曲线C截得弦长最短,求此时直线
过原点,且被曲线C截得弦长最短,求此时直线 的标准形式的参数方程;
的标准形式的参数方程;
(2) 是曲线C上的动点,求
是曲线C上的动点,求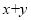 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末文科数学试卷(解析版) 题型:选择题
设非零向量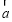 、
、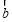 、
、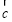 满足|
满足|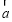 |=|
|=|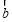 |=|
|=|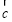 |,
|,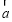 +
+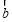 =
=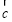 ,则向量
,则向量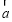 、
、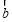 间的夹角为( )
间的夹角为( )
A.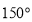 B.
B.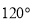 C.
C.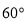 D.
D.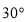
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江哈尔滨第六中学高二下学期期中考试理科数学卷(解析版) 题型:选择题
某单位为了了解用电量 (千瓦时)与气温
(千瓦时)与气温 (
( )之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温 | 18 | 13 | 10 |
|
用电量 | 24 | 34 | 38 | 64 |
由表中数据得线性回归方程 中
中 ,预测当气温为
,预测当气温为 时,用电量约为( )
时,用电量约为( )
A.58千瓦时 B.66千瓦时 C.68千瓦时 D.70千瓦时
(参考公式: )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com