
已知函数f(x)=log4(4x+1)+kx(k∈R)为偶函数.
(1)求k的值;
(2)若方程f(x)=log4(a·2x-a)有且只有一个根,求实数a的取值范围.
解 (1)∵f(x)为偶函数,∴f(-x)=f(x),
即log4(4-x+1)-kx=log4(4x+1)+kx,
即(2k+1)x=0,∴k=-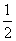 .
.
(2)依题意有log4(4x+1)-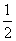 x=log4(a·2x-a),
x=log4(a·2x-a),
即
令t=2x,则(1-a)t2+at+1=0(*),
只需其有一正根即可满足题意.
①当a=1,t=-1时,不合题意.
②(*)式有一正一负根t1,t2,
即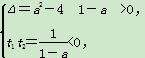
得a>1,经验证正根满足at-a>0,∴a>1.
③(*)式有相等两根,即Δ=0⇒a=±2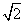 -2,
-2,
此时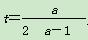 ,
,
若a=2(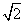 -1),则有
-1),则有 ,此时方程(1-a)t2+at+1=0无正根,故a=2(
,此时方程(1-a)t2+at+1=0无正根,故a=2(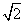 -1)舍去;
-1)舍去;
 因此a=-2(
因此a=-2(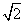 +1).
+1).
综上所述,a>1或a=-2-2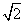 .
.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:高中数学 来源: 题型:
关于x的二次方程(m+3)x2-4mx+2m-1=0的两根异号,且负根的绝对值比正根大,那么实数m的取值范围是( )
A.-3<m<0 B.0<m<3
C.m<-3或m>0 D.m<0或m>3
查看答案和解析>>
科目:高中数学 来源: 题型:
某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为L1=5.06x-0.15x2和L2=2x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为( )
A.45.606万元 B.45.6万元
C.45.56万元 D.45.51万元
查看答案和解析>>
科目:高中数学 来源: 题型:
某化工厂打算投入一条新的生产线,但需要经环保部门审批同意方可投入生产.已知该生产线连续生产n年的累计产量为f(n)=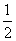 n(n+1)(2n+1)吨,但如果年产量超过150吨,会给环境造成危害,为保护环境,环保部门应给该厂这条生产线拟定最长的生产期限是( )
n(n+1)(2n+1)吨,但如果年产量超过150吨,会给环境造成危害,为保护环境,环保部门应给该厂这条生产线拟定最长的生产期限是( )
A.5年 B.6年
C.7年 D.8年
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=2x3-3x.
(1)求f(x)在区间[-2,1]上的最大值;
(2)若过点P(1,t)存在3条直线与曲线y=f(x)相切,求t的取值范围;
(3)问过点A(-1,2),B(2,10),C(0,2)分别存在几条直线与曲线y=f(x)相切?(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
某种产品每件成本为6元,每件售价为x元(6<x<11),年销售为u万件,若已知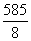 -u与
-u与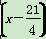 2成正比,且售价为10元时,年销量为28万件.
2成正比,且售价为10元时,年销量为28万件.
(1)求年销售利润y关于售价x的函数关系式;
(2)求售价为多少时,年利润最大,并求出最大年利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com