
【题目】已知命题 ![]() ,命题方程
,命题方程 ![]() 表示焦点在
表示焦点在 ![]() 轴上的双曲线.
轴上的双曲线.
(1)命题 ![]() 为真命题,求实数
为真命题,求实数 ![]() 的取值范围;
的取值范围;
(2)若命题“ ![]() ”为真,命题“
”为真,命题“ ![]() ”为假,求实数
”为假,求实数 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:命题 ![]() 为真,
为真, ![]()
(2)解:由题意命题 ![]() 一真一假,因此有
一真一假,因此有 ![]() 或
或 ![]() ,所以
,所以 ![]() 或
或 ![]()
【解析】(1)由题意结合真命题的定义解出一元二次不等式的解集即可求出k的取值范围。(2)利用复合命题的真假判断即可得出p , q 一真一假,结合题意即可得到关于k的不等式组解出即可。
【考点精析】关于本题考查的复合命题的真假和命题的真假判断与应用,需要了解“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真;两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知一元二次方程x2+(1+a)x+a+b+1=0的两个实根为x1,x2,且0<x1<1,x2>1,则 ![]() 的取值范围是( )
的取值范围是( )
A.(-2,- ![]() )
)
B.(-1,- ![]() )
)
C.(-2, ![]() )
)
D.(-1, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
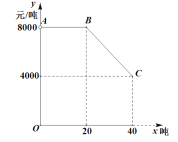
【题目】乔经理到老陈的果园里一次性采购一种水果,他俩商定:乔经理的采购价![]() (元/吨)与采购量
(元/吨)与采购量![]() (吨)之间函数关系的图像如图中的折线段
(吨)之间函数关系的图像如图中的折线段![]() 所示(不包含端点
所示(不包含端点![]() 但包含端点
但包含端点![]() ).
).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)已知老陈种植水果的成本是2800元/吨,那么乔经理的采购量为多少时,老陈在这次买卖中所获的利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.如果平面 ![]() 平面
平面 ![]() ,则
,则 ![]() 内任意一条直线必垂直于
内任意一条直线必垂直于 ![]()
B.若直线 ![]() 不平行于平面
不平行于平面 ![]() ,则
,则 ![]() 内不存在直线平行于直线
内不存在直线平行于直线 ![]()
C.如果平面 ![]() 不垂直于平面
不垂直于平面 ![]() ,那么平面
,那么平面 ![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面 ![]()
D.若直线 ![]() 不垂直于平面
不垂直于平面 ![]() ,则
,则 ![]() 内不存在直线垂直于直线
内不存在直线垂直于直线 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系中,曲线C1的参数方程为 ![]() (φ为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
(φ为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
(Ⅰ)求曲线C1的极坐标方程与曲线C2的直角坐标方程;
(Ⅱ)若直线θ= ![]() (ρ∈R)与曲线C1交于P,Q两点,求|PQ|的长度.
(ρ∈R)与曲线C1交于P,Q两点,求|PQ|的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥 ![]() 中,
中, ![]() 底面
底面 ![]() 分别是
分别是 ![]() 的中点,
的中点, ![]() 在
在 ![]() ,且
,且 ![]() .
.
(1)求证: ![]() 平面
平面 ![]() ;
;
(2)在线段 ![]() 上是否存在点
上是否存在点 ![]() ,使二面角
,使二面角 ![]() 的大小为
的大小为 ![]() ?若存在,求出
?若存在,求出 ![]() 的长;
的长;
若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A.命题“若 ![]() ,则
,则 ![]() ”的逆命题为“若
”的逆命题为“若 ![]() ,则
,则 ![]() ”
”
B.对于命题 ![]() ,使得
,使得 ![]() ,则
,则 ![]() ,则
,则 ![]()
C.“ ![]() ”是“
”是“ ![]() ”的充分不必要条件
”的充分不必要条件
D.若 ![]() 为假命题,则
为假命题,则 ![]() 均为假命题
均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电视台为了提高收视率而举办有奖问答活动,随机对该市15~65岁的人群抽样了 ![]() 人,回答问题统计结果及频率分布直方图如图表所示.
人,回答问题统计结果及频率分布直方图如图表所示.
(1)分别求出 ![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com