
| A. | [-1,0] | B. | [-1,+∞) | C. | [0,3] | D. | [3,+∞) |
分析 根据p≠q,不等式$\frac{f(p)-f(q)}{p-q}>0$恒成立,只需该函数在($\frac{1}{2}$,1)内的导数大于0恒成立.
解答 解:由题意,要使不等式$\frac{f(p)-f(q)}{p-q}>0$恒成立,
只需f′(x)>0在($\frac{1}{2}$,1)上恒成立.
因为f′(x)=2x+a-$\frac{1}{{x}^{2}}$,所以2x+a-$\frac{1}{{x}^{2}}$>0在($\frac{1}{2}$,1)上恒成立,
即a>$\frac{1}{{x}^{2}}$-2x,x∈($\frac{1}{2}$,1)恒成立,
令g(x)=$\frac{1}{{x}^{2}}$-2x,x∈($\frac{1}{2}$,1),g′(x)=-$\frac{2}{{x}^{3}}$-2<0,
g(x)在($\frac{1}{2}$,1)递减,g(x)<g($\frac{1}{2}$)=3
只需a≥3,
故选:D.
点评 本题考查了导数的几何意义以及不等式恒成立问题的基本思路.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?n∈N,n2<2n | B. | ?n∈N,n2≥2n | C. | ?n∈N,n2≥2n | D. | ?n∈N,n2>2n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 84 | B. | 78 | C. | 81 | D. | 96 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 增加了一项$\frac{1}{{2({k+1})}}$ | B. | 增加了两项$\frac{1}{2k+1}$和$\frac{1}{{2({k+1})}}$ | ||
| C. | 增加了B中两项,但又少了一项$\frac{1}{k+1}$ | D. | 增加了A中一项,但又少了一项$\frac{1}{k+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
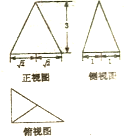
| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $6\sqrt{2}$ | D. | $6\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com