练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．某几何体的三视图如图所示，则其体积为6π．      
      

    分析 由已知中的三视图，可得该几何体是一个以俯视图为底面的半圆锥，代入锥体体积公式，可得答案．

    解答 解：由已知中的三视图，可得该几何体是一个以俯视图为底面的半圆锥，
    其底面面积S=$\frac{1}{2}π•{3}^{2}$=$\frac{9π}{2}$，
    高h=4，
    故体积V=$\frac{1}{3}Sh$=6π，
    故答案为：6π

    点评 本题考查的知识点是圆锥的体积和表面积，简单几何体的三视图，难度基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    11．已知命题q：?x∈R，cosx≤1，则￢q是（　　）
    A．?x∈R，cosx≥1B．?x∈R，cosx＞1C．?x0∈R，cosx0≥1D．?x0∈R，cosx0＞1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．若$x∈（{e，{e^2}}），a=lnx，b={（{\frac{1}{2}}）^{lnx}}，c={e^{lnx}}$，则a，b，c的大小关系为（　　）
    A．c＞b＞aB．c＞a＞bC．a＞b＞cD．b＞c＞a

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．随着经济模式的改变，微商和电商已成为当今城乡一种新型的购销平台．已知经销某种商品的电商在任何一个销售季度内，每售出1吨该商品可获利润0.5万元，未售出的商品，每1吨亏损0.3万元．根据往年的销售经验，得到一个销售季度内市场需求量的频率分布直方图如右图所示．已知电商为下一个销售季度筹备了130吨该商品．现以x（单位：吨，100≤x≤150）表示下一个销售季度的市场需求量，T（单位：万元）表示该电商下一个销售季度内经销该商品获得的利润．
    （Ⅰ）视x分布在各区间内的频率为相应的概率，求P（x≥120）
    （Ⅱ）将T表示为x的函数，求出该函数表达式；
    （Ⅲ）在频率分布直方图的市场需求量分组中，以各组的区间中点值（组中值）代表该组的各个值，并以市场需求量落入该区间的频率作为市场需求量取该组中值的概率（例如x∈[100，110），则取x=105，且x=105的概率等于市场需求量落入100，110）的频率），求T的分布列及数学期望E（T）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

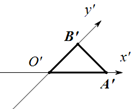    16．如图一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′，若O′B′=B′A′=1，那么原△ABO的面积是（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．$\sqrt{2}$D．2$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=x2-2ax+2（a∈R）．
    （1）若a=1时，求函数f（x）在x∈[-1，2]上的最大值；
    （2）当x∈[-1，+∞）时，f（x）≥a恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．下列结论正确的是（　　）
    A．事件A的概率P（A）必有0＜P（A）＜1
    B．事件A的概率P（A）=0.999，则事件A是必然事件
    C．用某种药物对患有胃溃疡的500名病人治疗，结果有380人有明显的疗效，现有胃溃疡的病人服用此药，则估计其有明显的疗效的可能性为76%
    D．某奖券中奖率为50%，则某人购买此券10张，一定有5张中奖

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．若函数$f（x）={x^2}+ax+\frac{1}{x}$在$（{\frac{1}{2}\;\;，\;\;1}）$内任取两个实数p，q，且p≠q，不等式$\frac{f（p）-f（q）}{p-q}＞0$恒成立，则a的取值范围是（　　）
    A．[-1，0]B．[-1，+∞）C．[0，3]D．[3，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知函数f（x）=x-alnx，当x＞1时，f（x）＞0恒成立，则实数a的取值范围是（　　）
    A．（1，+∞）B．（-∞，1）C．（e，+∞）D．（-∞，e）

    查看答案和解析>>

    同步练习册答案