
分析 (1)求得f(x)的对称轴,与区间的端点比较,可得f(-1)取得最大值;
(2)求出二次函数的对称轴,讨论当a≤-1时,当a>-1时,运用单调性,可得最小值,由题意可得f(x)min≥a,即可得到所求a的范围.
解答 解:(1)若a=1,则f(x)=x2-2x+2,
对称轴为x=1,x∈[-1,2],
由1与-1的距离比1与2的距离大,
则当x=-1时,函数f(x)的最大值为5;
(2)函数f(x)=x2-2ax+2(a∈R),
对称轴为x=a,x∈[-1,+∞),
当a≤-1时,f(x)在[-1,+∞)递增,
可得f(x)的最小值为f(-1)=3+2a;
由3+2a≥a,解得a≥-3,
则-3≤a≤-1;
当a>-1时,f(x)的最小值为f(a)=2-a2,
2-a2≥a,解得-2≤a≤1,
即为-1<a≤1,
综上可得-3≤a≤1.
点评 本题考查二次函数在闭区间上的最值解法,注意对称轴和区间的关系,同时考查不等式恒成立问题的解法,注意运用分类讨论思想方法,以及函数的单调性,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
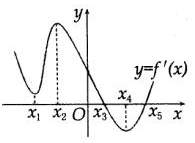 如图是函数y=f(x)的导函数y=f′(x)的图象,下列关于函数y=f(x)的极值和单调性的说法中,正确的个数是( )
如图是函数y=f(x)的导函数y=f′(x)的图象,下列关于函数y=f(x)的极值和单调性的说法中,正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (0,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
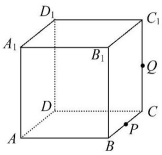 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是①②④(写出所有正确命题的编号).
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是①②④(写出所有正确命题的编号).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 84 | B. | 78 | C. | 81 | D. | 96 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com