练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．已知直线l1：ax+4y-1=0，l2：x+ay-$\frac{1}{2}$=0，若l1∥l2，则实数a=-2．

    分析 利用直线平行的性质求解．

    解答 解：∵直线l1：ax+4y-1=0，l2：x+ay-$\frac{1}{2}$=0，
    ∴$\frac{a}{1}=\frac{4}{a}≠\frac{-1}{-\frac{1}{2}}$，
    解得a=-2（a=2时，两条直线重合，舍去）．
    故答案为：-2．

    点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意直线平行的性质的灵活运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．漳州市“网约车”的现行计价标准是：路程在2km以内（含2km）按起步价8元收取，超过2km后的路程按1.9元/km收取，但超过10km后的路程需加收50%的返空费（即单价为1.9×（1+50%）=2.85元）．
    （1）将某乘客搭乘一次“网约车”的费用f（x）（单位：元）表示为行程x（0＜x≤60，单位：km）的分段函数；
    （2）某乘客的行程为16km，他准备先乘一辆“网约车”行驶8km后，再换乘另一辆“网约车”完成余下行程，请问：他这样做是否比只乘一辆“网约车”完成全部行程更省钱？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知命题q：?x∈R，cosx≤1，则￢q是（　　）
    A．?x∈R，cosx≥1B．?x∈R，cosx＞1C．?x0∈R，cosx0≥1D．?x0∈R，cosx0＞1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．设m，n是两条不同的直线，α，β是两个不同的平面，下列说法正确的是（　　）
    A．若m∥α，α∩β=n，则 m∥nB．若m∥α，m⊥n，则n⊥α
    C．若m⊥α，n⊥α，则m∥nD．若m?α，n?β，α⊥β，则m⊥n

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

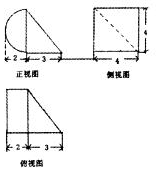
    15．圆柱被一个平面截去一部分后与一个四棱锥组成的几何体的三视图如图所示，则该几何体的体积为（　　）
    A．4π+8B．8π+16C．16π+16D．16π+48

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．在直三棱柱ABC-A1B1C1中，D，E分别是BC，A1B1的中点．
    （1）求证：DE∥平面ACC1A1；
    （2）设M为AB上一点，且AM=$\frac{1}{4}$AB，若直三棱柱ABC-A1B1C1的所有棱长均相等，求直线DE与直线A1M所成角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．若$x∈（{e，{e^2}}），a=lnx，b={（{\frac{1}{2}}）^{lnx}}，c={e^{lnx}}$，则a，b，c的大小关系为（　　）
    A．c＞b＞aB．c＞a＞bC．a＞b＞cD．b＞c＞a

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．随着经济模式的改变，微商和电商已成为当今城乡一种新型的购销平台．已知经销某种商品的电商在任何一个销售季度内，每售出1吨该商品可获利润0.5万元，未售出的商品，每1吨亏损0.3万元．根据往年的销售经验，得到一个销售季度内市场需求量的频率分布直方图如右图所示．已知电商为下一个销售季度筹备了130吨该商品．现以x（单位：吨，100≤x≤150）表示下一个销售季度的市场需求量，T（单位：万元）表示该电商下一个销售季度内经销该商品获得的利润．
    （Ⅰ）视x分布在各区间内的频率为相应的概率，求P（x≥120）
    （Ⅱ）将T表示为x的函数，求出该函数表达式；
    （Ⅲ）在频率分布直方图的市场需求量分组中，以各组的区间中点值（组中值）代表该组的各个值，并以市场需求量落入该区间的频率作为市场需求量取该组中值的概率（例如x∈[100，110），则取x=105，且x=105的概率等于市场需求量落入100，110）的频率），求T的分布列及数学期望E（T）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．若函数$f（x）={x^2}+ax+\frac{1}{x}$在$（{\frac{1}{2}\;\;，\;\;1}）$内任取两个实数p，q，且p≠q，不等式$\frac{f（p）-f（q）}{p-q}＞0$恒成立，则a的取值范围是（　　）
    A．[-1，0]B．[-1，+∞）C．[0，3]D．[3，+∞）

    查看答案和解析>>

    同步练习册答案