
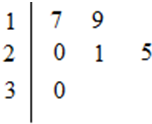
 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.分析 (I)利用平均值的计算公式即可得出.
(II)由(Ⅰ)知样本中优秀工人占的比例为$\frac{2}{6}$,即可故推断该车间12名工人中的优秀工人.
(III)利用超几何分布列的计算公式及其数学期望即可得出.
解答 解:(Ⅰ)样本均值为$\frac{17+19+20+21+25+30}{6}$=$\frac{132}{6}$=22.
(Ⅱ) 由(Ⅰ)知样本中优秀工人占的比例为$\frac{2}{6}$=$\frac{1}{3}$,
故推断该车间12名工人中有12×$\frac{1}{3}$=4名优秀工人.
(Ⅲ) ξ的可能取值为0,1,2.
$p(ξ=0)=\frac{C_4^0C_8^2}{{C_{12}^2}}=\frac{14}{33}$,$p(ξ=1)=\frac{C_4^1C_8^1}{{C_{12}^2}}=\frac{16}{33}$,$p(ξ=2)=\frac{C_4^2C_8^0}{{C_{12}^2}}=\frac{3}{33}$.
$E(ξ)=0×\frac{14}{33}+1×\frac{16}{33}+2×\frac{3}{33}=\frac{22}{33}$.
点评 本题考查了超几何分布列的计算公式及其数学期望、茎叶图及其应用,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x,g(x)=($\sqrt{x}$)2 | B. | f(x)=x2+1,g(t)=t2+1 | C. | f(x)=1,g(x)=$\frac{x}{x}$ | D. | f(x)=x,g(x)=|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4${∫}_{0}^{a}$xf(x)dx | B. | 2${∫}_{0}^{a}$x[f(x)+f(-x)]dx | C. | 0 | D. | 以上都不正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com