
分析 (1)利用函数的对称轴以及方程的根的关系,即可求解函数的表达式.
(2)求出函数的对称轴,通过m,n与对称轴讨论,结合函数的定义域与值域,列出方程求解即可.
解答 解:∵函数满足f(-x+5)=f(x-3),∴$f(x)的对称轴为x=1∴-\frac{b}{2a}=1$,
因为方程f(x)=x有等根,即ax2+bx-x=0,有重根,∴△=0,可得a=$-\frac{1}{2}$,
可得b=1,
∴二次函数f(x)=-$\frac{1}{2}$x2+x.
(2)二次函数f(x)=-$\frac{1}{2}$x2+x.的对称轴为x=1,
当m<n<1时,$\left\{\begin{array}{l}{f(m)=3m}\\{f(n)=3n}\end{array}\right.$,∴$\left\{\begin{array}{l}{n=0}\\{m=-4}\end{array}\right.$;
当1<m<n时,$\left\{\begin{array}{l}{f(m)=3n}\\{f(n)=3m}\end{array}\right.$,方程无解;
当n>1>m时,f(1)=$\frac{1}{2}$=3n,无解;
综上所述,n=0,m=-4.
点评 本题考查二次函数的简单性质的应用,函数的对称轴与函数的定义域与值域的关系,考查分类讨论思想以及转化思想的应用,考查计算能力.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:解答题
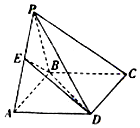 如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中点,且PA=PB=AB=2,BC=$\sqrt{2}$.
如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中点,且PA=PB=AB=2,BC=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
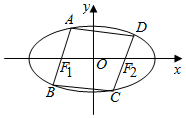 如图所示,椭圆C:$\frac{{x}^{2}}{4}$+y2=1,左右焦点分别记作F1,F2,过F1,F2分别作直线l1,l2交椭圆AB,CD,且l1∥l2.
如图所示,椭圆C:$\frac{{x}^{2}}{4}$+y2=1,左右焦点分别记作F1,F2,过F1,F2分别作直线l1,l2交椭圆AB,CD,且l1∥l2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
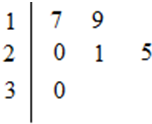 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
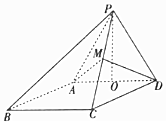 如图,四棱锥P-ABCD,底面ABCD是∠ABC=60°的菱形,侧面PAD是边长为2的正三角形,O是AD的中点,M为PC的中点.
如图,四棱锥P-ABCD,底面ABCD是∠ABC=60°的菱形,侧面PAD是边长为2的正三角形,O是AD的中点,M为PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com