
分析 (I)根据已知中在区间$[-\frac{π}{2},π]$上的函数y=f(x)的图象关于直线$x=\frac{π}{4}$对称,当$\frac{π}{4}≤x≤π$时,f(x)=sinx,我们可根据函数图象对称变换法则求出函数y=f(x)的函数表达式;
(II)作函数f(x)的图象,分析函数的图象得到函数的性质,分类讨论后,结合方程在a取某一确定值时所求得的所有解的和记为Ma,即可得到答案.
解答 解:(I)对于任意的-$\frac{π}{2}$≤x≤$\frac{π}{4}$,都有$\frac{π}{4}$≤$\frac{π}{2}$-x≤π时,…(2分)
由函数y=f(x)的图象关于直线$x=\frac{π}{4}$对称得f(x)=f($\frac{π}{2}$-x)=sin($\frac{π}{2}$-x)=cosx…(5分)
所以f(x)=$\left\{\begin{array}{l}{sinx,x∈[\frac{π}{4},π]}\\{cosx,x∈[-\frac{π}{2},\frac{π}{4})}\end{array}\right.$…(6分)
(II)作出函数f(x)的图象(如右下图所示)可知,若方程f(x)=a有解,则a∈[0,1]
①当0≤a<$\frac{\sqrt{2}}{2}$或a=1时,f(x)=a有两解,Ma=$\frac{π}{2}$…(8分)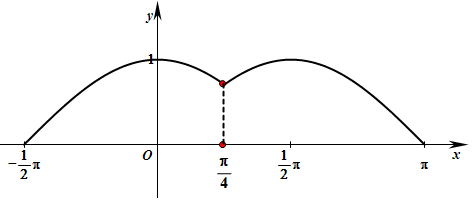
②当a=$\frac{\sqrt{2}}{2}$时,f(x)=a有三解,Ma=$\frac{3π}{4}$ …(10分)
③当$\frac{\sqrt{2}}{2}<a<1$时,f(x)=a有四解,Ma=π…(12分)
点评 本题考查的知识点是函数解析式的求法--图象变换法,根的存在性及根的个数的判断,其中根据条件结合对称变换法则,求出函数的解析式是解答本题的关键.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:解答题
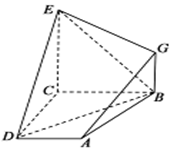 如图,已知四边形BCD和BCEG均为直角梯形,AD∥EG、CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=2AD,CE=2BG.求证:
如图,已知四边形BCD和BCEG均为直角梯形,AD∥EG、CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=2AD,CE=2BG.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0或$\sqrt{3}$ | B. | 0或3 | C. | 3或$\sqrt{3}$ | D. | 1或3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{1-{m}^{2}}}{m}$ | B. | -$\frac{\sqrt{1-{m}^{2}}}{m}$ | C. | $\frac{m}{\sqrt{1-{m}^{2}}}$ | D. | -$\frac{m}{\sqrt{1-{m}^{2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
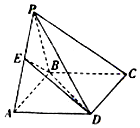 如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中点,且PA=PB=AB=2,BC=$\sqrt{2}$.
如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中点,且PA=PB=AB=2,BC=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
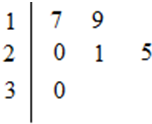 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com