
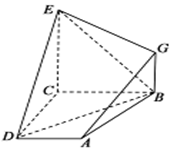
 如图,已知四边形BCD和BCEG均为直角梯形,AD∥EG、CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=2AD,CE=2BG.求证:
如图,已知四边形BCD和BCEG均为直角梯形,AD∥EG、CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=2AD,CE=2BG.求证:分析 (Ⅰ)利用面面垂直的性质,证明EC⊥平面ABCD,利用线面垂直的性质证明EC⊥CD;
(Ⅱ)在平面BCEG中,过G作GN⊥CE交BE于M,连DM,证明四边形ADMG为平行四边形,可得AG∥DM,即可证明AG∥平面BDE.
解答 证明:如图示: ,
,
(Ⅰ)由平面ABCD⊥平面BCEG,
平面ABCD∩平面BCEG=BC,CE⊥BC,CE?平面BCEG,
∴EC⊥平面ABCD,又CD?平面BCDA,故 EC⊥CD;
(Ⅱ)在平面BCEG中,过G作GN⊥CE交BE于M,
连结DM,则由已知知;MG=MN,MN∥BC∥DA,且$MN=AD=\frac{1}{2}BC$,
∴MG∥AD,MG=AD,故四边形ADMG为平行四边形,
∴AG∥DM,
∵DM⊆平面BDE,AG?平面BDE,
∴AG∥平面BDE.
点评 本题考查面面垂直、线面平行,考查学生分析解决问题的能力,正确运用面面垂直、线面平行的判定定理是关键.


科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x≤3} | B. | {x|x<-2或x>4} | C. | {x|-3≤x≤4} | D. | {x|x<-3或x>4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,4] | B. | [0,4] | C. | (-∞,0]∪[4,+∞) | D. | (-∞,0)∪(4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com