
分析 令y=x可得f(x+f(x)+xf(x))=x+f(x)+xf(x),令x+f(x)+xf(x)=c,则f(c)=c,代入(1)可得f(2c+c2)=2c+c2.对c的符号进行讨论得出c=0即x+f(x)+xf(x)=0,从而得出f(x)的解析式.
解答 解:令y=x得f(x+f(x)+xf(x))=x+f(x)+xf(x),
令x+f(x)+xf(x)=c,则f(c)=c,
带入(1)得f(2c+c2)=2c+c2.∵2+c>2+(-1)=1,∴2c+c2=c(2+c)与c同号.
若c>0,则2c+c2>c,但$\frac{{f(2c+{c^2})}}{{2c+{c^2}}}=\frac{f(c)}{c}=1$,与$\frac{f(x)}{x}$在x>0时严格递增相矛盾,
若c<0,同样导出矛盾,
∴c=0,从而对一切x∈S有x+f(x)+xf(x)=0,
∴$f(x)=-\frac{x}{x+1}$.
点评 本题考查了抽象函数的性质的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-\frac{3}{2}]∪[-1,+∞)$ | B. | $(-∞,-\frac{5}{2}]∪[-1,+∞)$ | C. | $[-\frac{5}{2},-\frac{3}{2}]$ | D. | $[-\frac{3}{2},-1]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}$ | B. | $-\frac{9}{8}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{2}{3}π$ | B. | $\frac{π}{3}$ | C. | $\frac{2}{3}π$ | D. | $-\frac{2}{3}π$或$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
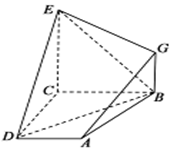 如图,已知四边形BCD和BCEG均为直角梯形,AD∥EG、CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=2AD,CE=2BG.求证:
如图,已知四边形BCD和BCEG均为直角梯形,AD∥EG、CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=2AD,CE=2BG.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com