
【题目】已知α∈(0, ![]() ),β∈(0,π),且tan(α﹣β)=
),β∈(0,π),且tan(α﹣β)= ![]() ,tanβ=﹣
,tanβ=﹣ ![]() .
.
(1)求tanα;
(2)求2α﹣β的值.
【答案】
(1)解:∵2α﹣β=2(α﹣β)+β,
又tan(α﹣β)= ![]() ,
,
∴tan2(α﹣β)= ![]() =
= ![]() .
.
故tan(2α﹣β)=tan[2(α﹣β)+β]= ![]() =
= 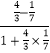 =1.
=1.
∴tanα=tan[(α﹣β)+β]= ![]() =
= ![]() .
.
(2)解:∵0<α< ![]() ,
,
∴0<2α< ![]() .
.
又∵tanβ=﹣ ![]() ,且β∈(0,π)β∈(
,且β∈(0,π)β∈( ![]() ,π)﹣β∈(﹣π,﹣
,π)﹣β∈(﹣π,﹣ ![]() ).
).
∴2α﹣β∈(﹣π,0).又由(1)可得tan(2α﹣β)=1,
∴2α﹣β=﹣ ![]() .
.
【解析】(1)观察角度的关系发现2α﹣β=2(α﹣β)+β,求出tan2(α﹣β),然后利用两角和的正切函数求出tan(2α﹣β),进而可求tanα的值.(2)再根据tanα、tanβ的值确定α,β的具体范围,进而确定2α﹣β的范围,就可以根据特殊角的三角函数值求出结果.
【考点精析】解答此题的关键在于理解两角和与差的正切公式的相关知识,掌握两角和与差的正切公式:![]() .
.


科目:高中数学 来源: 题型:
【题目】某厂生产的产品在出厂前都要做质量检测,每件一等品都能通过检测,每件二等品通过检测的概率为![]() .现有
.现有![]() 件产品,其中
件产品,其中![]() 件是一等品,
件是一等品, ![]() 件是二等品.
件是二等品.
(Ⅰ)随机选取![]() 件产品,设至少有一件通过检测为事件
件产品,设至少有一件通过检测为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(Ⅱ)随机选取![]() 件产品,其中一等品的件数记为
件产品,其中一等品的件数记为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosωx,sinωx),
=(cosωx,sinωx), ![]() =(cosωx,
=(cosωx, ![]() cosωx),其中ω>0,设函数f(x)=
cosωx),其中ω>0,设函数f(x)= ![]()
![]() .
.
(1)若函数f(x)的最小正周期是π,求函数f(x)的单调递增区间;
(2)若函数f(x)的图象的一个对称中心的横坐标为 ![]() ,求ω的最小值.
,求ω的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
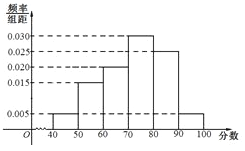
【题目】上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中抽取80名学生的数学成绩(均为整数)的频率分布直方图如图所示.
(Ⅰ)估计这次月考数学成绩的平均分和众数;
(Ⅱ)假设抽出学生的数学成绩在![]() 段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为
段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2015高考湖北】如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.
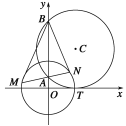
(1)圆C的标准方程为________.
(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:
①![]() =
=![]() ;②
;②![]() -
-![]() =2;
=2;
③![]() +
+![]() =2
=2![]() .
.
其中正确结论的序号是________(写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(Ⅰ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅱ)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】Sn为数列{an}的前n项和,Sn=2an﹣2(n∈N+)
(1)求{an}的通项公式;
(2)若bn=3nan,求数列{bn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com