
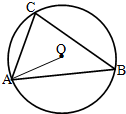
 如图所示,在△ABC中,AB=4,AC=2,若O为△ABC的外心.
如图所示,在△ABC中,AB=4,AC=2,若O为△ABC的外心.分析 (Ⅰ)由垂径分弦定理得$|\overrightarrow{AO}|cos∠OAC=\frac{1}{2}|\overrightarrow{AC}|$,利用数量积运算性质即可得出;
(Ⅱ)利用向量三角形法则可得:$\overrightarrow{AO}•\overrightarrow{CB}=\overrightarrow{AO•}(\overrightarrow{AB}-\overrightarrow{AC})$,展开利用(I)的结论即可得出;
(III)利用已知可得:$|\overrightarrow{PA}|=|\overrightarrow{PB}|=|\overrightarrow{PC}|$,即点P与O点重合.
解答 解:(Ⅰ)由垂径分弦定理得$|\overrightarrow{AO}|cos∠OAC=\frac{1}{2}|\overrightarrow{AC}|$,
∴$\overrightarrow{AO}•\overrightarrow{AC}=|\overrightarrow{AC}|•|\overrightarrow{AO}|cos∠OAC$=$\frac{1}{2}|\overrightarrow{AC}{|^2}=2$.
(Ⅱ)同样$\overrightarrow{AO}•\overrightarrow{CB}=\overrightarrow{AO•}(\overrightarrow{AB}-\overrightarrow{AC})$=$|\overrightarrow{AB}|•|\overrightarrow{AO}|cos∠OAB-|\overrightarrow{AC}|•|\overrightarrow{AO}|cos∠OAC$=$\frac{1}{2}[|\overrightarrow{AB}{|^2}-|\overrightarrow{AC}{|^2}]=8-2=6$.
(Ⅲ)由$(\overrightarrow{PA}+\overrightarrow{PB})•\overrightarrow{AB}=(\overrightarrow{PA}+\overrightarrow{PB})•(\overrightarrow{PB}-\overrightarrow{PA})={\overrightarrow{PB}^2}-{\overrightarrow{PA}^2}=0$$⇒|\overrightarrow{PA}|=|\overrightarrow{PB}|$
同理有:$|\overrightarrow{PB}|=|\overrightarrow{PC}|$,$|\overrightarrow{PC}|=|\overrightarrow{PA}|$,
∴$|\overrightarrow{PA}|=|\overrightarrow{PB}|=|\overrightarrow{PC}|$,即点P与O点重合,
∴点P为△ABC的外心.
点评 本题考查了向量垂直与数量积的关系、三角形外心的性质、圆的垂径定理,考查了推理能力与计算能力,属于中档题.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,3) | B. | (-1,3) | C. | [-1,3] | D. | (-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
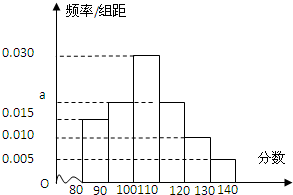 某校高一(1)班共有54人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在[100,120]内的学生人数为( )
某校高一(1)班共有54人,如图是该班期中考试数学成绩的频率分布直方图,则成绩在[100,120]内的学生人数为( )| A. | 36 | B. | 27 | C. | 22 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com