
【题目】已知数列![]() ,若对任意
,若对任意![]() ,都有
,都有![]() 成立,则称数列
成立,则称数列![]() 为“差增数列”.
为“差增数列”.
(1)试判断数列![]() 是否为“差增数列”,并说明理由;
是否为“差增数列”,并说明理由;
(2)若数列![]() 为“差增数列”,且
为“差增数列”,且![]() ,
,![]() ,对于给定的正整数m,当
,对于给定的正整数m,当![]() ,项数k的最大值为20时,求m的所有可能取值的集合;
,项数k的最大值为20时,求m的所有可能取值的集合;
(3)若数列![]() 为“差增数列”,
为“差增数列”,![]() ,且
,且![]() ,证明:
,证明:![]() .
.
【答案】(1)是;见解析(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)数列![]() 是“差增数列”.由新定义可知,只要证明
是“差增数列”.由新定义可知,只要证明![]() >an+1即可;
>an+1即可;
(2)由新定义可得对任意的n∈N*,an+2﹣an+1>an+1﹣an恒成立,可令bn=an+1﹣an(n≥1),运用累加法,结合等差数列的求和公式可得an,由于1≤n≤19,结合条件可得m的取值集合;
(3)运用反证法证明,假设x1010x1011≥1,由题意可得x1x2…x2020=1,![]() <
<![]() ,运用不等式的性质推得x1009x1012>1,即可得到矛盾,进而得证.
,运用不等式的性质推得x1009x1012>1,即可得到矛盾,进而得证.
解:(1)数列![]() 是“差增数列”.
是“差增数列”.
因为任意的n∈N*,都有an+an+2=n2+(n+2)2=2n2+4n+4=2(n+1)2+2>2(n+1)2=2an+1,
即![]() >an+1成立,
>an+1成立,
所以数列![]() 是“差增数列”;
是“差增数列”;
(2)由已知,对任意的n∈N*,an+2﹣an+1>an+1﹣an恒成立.
可令bn=an+1﹣an(n≥1),则bn∈N,且bn<bn+1,
又an=m,要使项数k达到最大,且最大值为20时,必须bn(1≤n≤18)最小.
而b1=0,故b2=1,b3=2,…,bn=n﹣1.
所以an﹣a1=b1+b2+…+bn﹣1=0+1+2+…+(n﹣2)=![]() (n﹣1)(n﹣2),
(n﹣1)(n﹣2),
即当1≤n≤19时,an=1+![]() ,a19=154,因为k的最大值为20,
,a19=154,因为k的最大值为20,
所以18≤a20﹣a19<18+19,即18≤m﹣154<18+19,
所以m的所有可能取值的集合为{m|172≤m<191,m∈N*}.
(3)证明:(反证法)假设x1010x1011≥1.由已知可得xn(n=1,2,…,2020)均为正数,且x1x2…x2020=1,![]() <
<![]() .
.
而由![]() <
<![]() 可得
可得![]() <
<![]() <
<![]() ,
,
即x1010x1011<x1009x1012,所以x1009x1012>1.
又![]() =
=![]()
![]() <
<![]()
![]() =
=![]() ,即x1008x1013>1,
,即x1008x1013>1,
同理可证x1007x1014>1,…,x1x2020>1,
因此x1x2…x2020>1,这与已知矛盾,
所以x1010x1011<1.


科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的离心率为
)的离心率为![]() ,过右焦点且垂直于长轴的直线与椭圆C交于P,Q两点,且
,过右焦点且垂直于长轴的直线与椭圆C交于P,Q两点,且![]() .
.
(1)求椭圆C的方程;
(2)A,B是椭圆C上的两个不同点,若直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() (以O为坐标原点),M是
(以O为坐标原点),M是![]() 的中点,连接
的中点,连接![]() 并延长交椭圆C于点N,求
并延长交椭圆C于点N,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ).
).
(1)当![]() 时,若函数
时,若函数![]() 在
在![]() 上有两个零点,求
上有两个零点,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,是否存在
时,是否存在![]() ,使得不等式
,使得不等式![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设无穷数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在数列![]() 的一个无穷子数列
的一个无穷子数列![]() ,使
,使![]() 对一切
对一切![]() 均成立?若存在,请写出数列
均成立?若存在,请写出数列![]() 的所有通项公式;若不存在,请说明理由.
的所有通项公式;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() ,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)在平面直角坐标系xOy中,A(﹣2,0),B(0,﹣2),M是曲线C上任意一点,求△ABM面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区城乡居民储蓄存款年底余额(单位:亿元)如图所示,下列判断一定不正确的是( )
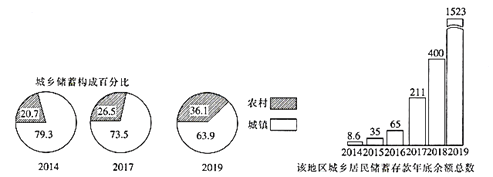
A.城乡居民储蓄存款年底余额逐年增长
B.农村居民的存款年底余额所占比重逐年上升
C.到2019年农村居民存款年底总余额已超过了城镇居民存款年底总余额
D.城镇居民存款年底余额所占的比重逐年下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱维![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上点
上点![]() 是
是![]() 的重心.
的重心.
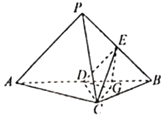
(1)若![]() 是
是![]() 的中点,证明
的中点,证明![]() 面
面![]() ;
;
(2)是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,若存在,求
,若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com