练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某舞台灯光设计师为了在地板上设计图案，他把一端向下发光的光源和支架之间的角度固定为θ角，支架的一端固定在地板的中心位置，支架的另一端固定在天花板的适当位置，当光源围绕支架以θ角快速旋转时，地板上可能出现的图案有（ ）

    A.椭圆 B.抛物线 C.圆 D.以上均有可能

    D

    【解析】

    试题分析：根据圆锥曲线的定义，设支架与地板的夹角为α，分别讨论当α=90°时，当θ＜α＜90°时，当α=θ时，当α＜θ时，地板上出现的图案的形状，可得答案．

    【解析】
    设支架与地板的夹角为α，

    当α=90°时，地板上出现的图案为圆；

    当θ＜α＜90°时，地板上出现的图案为椭圆；

    当α=θ时，地板上出现的图案为抛物线；

    当α＜θ时，地板上出现的图案为双曲线的一支；

    故选：D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014-2015学年天津市高三上学期第二次月考文科数学试卷（解析版） 题型：填空题

    若对任意，不等式恒成立，则实数的范围是 ____

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年上海市高二上学期第一次月考数学试卷（解析版） 题型：解答题

    已知数列满足

    （1）求数列的通项公式；（2）求数列的前项和

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修4-1 2.3柱面与平面的截面练习卷（解析版） 题型：解答题

    如图，圆柱的轴截面ABCD是正方形，点E在底面的圆周上，AF⊥DE，F是垂足．

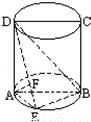
    （1）求证：AF⊥DB；

    （2）如果圆柱与三棱锥D﹣ABE的体积的比等于3π，求直线DE与平面ABCD所成的角．

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修4-1 2.3柱面与平面的截面练习卷（解析版） 题型：填空题

    工人师傅在如图1的一块矩形铁皮的中间画了一条曲线，并沿曲线剪开，将所得的两部分卷成圆柱状，如图2，然后将其对接，可做成一个直角的“拐脖”，如图3．对工人师傅所画的曲线，有如下说法：

    （1）是一段抛物线；

    （2）是一段双曲线；

    （3）是一段正弦曲线；

    （4）是一段余弦曲线；

    （5）是一段圆弧．

    则正确的说法序号是 ．

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系（解析版） 题型：填空题

    设P、A、B、C是球O表面上的四个点，PA、PB、PC两两垂直，且PA=3，PB=4，PC=5，则球的半径为 ．

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系（解析版） 题型：选择题

    下列四个命题中错误的个数是（ ）

    ①经过球面上任意两点，可以作且只可以作一个球的大圆；

    ②球面积是它大圆面积的四倍；

    ③球面上两点的球面距离，是这两点所在截面圆上以这两点为端点的劣弧的长．

    A.0 B.1 C.2 D.3

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-3 2.2超几何分布练习卷（解析版） 题型：解答题

    甲有一个箱子，里面放有x个红球，y个白球（x，y≥0，且x+y=4）；乙有一个箱子，里面放有2个红球，1个白球，1个黄球．现在甲从箱子任取2个球，乙从箱子里在取1个球，若取出的3个球颜色全不相同，则甲获胜．

    （1）试问甲如何安排箱子里两种颜色的个数，才能使自己获胜的概率最大？

    （2）在（1）的条件下，求取出的3个球中红球个数的数学期望．

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷（解析版） 题型：?????

    设y=﹣2exsinx，则y′等于（ ）

    A.﹣2excosx B.﹣2exsinx C.2exsinx D.﹣2ex（sinx+cosx）

    查看答案和解析>>

    同步练习册答案