
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足.
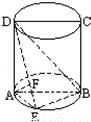
(1)求证:AF⊥DB;
(2)如果圆柱与三棱锥D﹣ABE的体积的比等于3π,求直线DE与平面ABCD所成的角.
(1)见解析;(2)arcctg( /5)
/5)
【解析】
试题分析:(1)欲证AF⊥DB,先证AF⊥平面DEB,根据线面垂直的判定定理可知只需证EB⊥AF,AF⊥DE,且EB∩DE=E,即可证得线面垂直;
(2)点E作EH⊥AB,H是垂足,连接DH,易证∠EDH是DE与平面ABCD所成的角,在三角形EDH中求出此角即可.
(1)证明:根据圆柱性质,DA⊥平面ABE.
∵EB?平面ABE,
∴DA⊥EB.
∵AB是圆柱底面的直径,点E在圆周上,
∴AE⊥EB,又AE∩AD=A,
故得EB⊥平面DAE.
∵AF?平面DAE,
∴EB⊥AF.
又AF⊥DE,且EB∩DE=E,
故得AF⊥平面DEB.
∵DB?平面DEB,
∴AF⊥DB.
(2)【解析】
过点E作EH⊥AB,H是垂足,连接DH.
根据圆柱性质,平面ABCD⊥平面ABE,AB是交线.且EH?平面ABE,所以EH⊥平面ABCD.
又DH?平面ABCD,所以DH是ED在平面ABCD上的射影,从而∠EDH是DE与平面ABCD所成的角.
设圆柱的底面半径为R,则DA=AB=2R,于是
V圆柱=2πR3, .
.
由V圆柱:VD﹣ABE=3π,得EH=R,可知H是圆柱底面的圆心,
AH=R,
DH=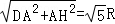
∴∠EDH=arcctg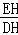 =arcctg(
=arcctg( /5),
/5),




 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源:2014-2015学年安徽省淮北市高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
已知实数x,y满足 设
设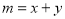 ,若
,若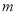 的最大值为6,则
的最大值为6,则 的最小值为( )
的最小值为( )
A.—3 B.—2 C.—1 D.0
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市高二上学期第一次月考数学试卷(解析版) 题型:选择题
下列命题中正确的是 ( )
A.公差为0的等差数列是等比数列
B.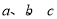 成等比数列的充要条件是
成等比数列的充要条件是
C.公比 的等比数列是递减数列
的等比数列是递减数列
D.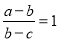 是
是 成等差数列的充分不必要条件
成等差数列的充分不必要条件
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.3柱面与平面的截面练习卷(解析版) 题型:填空题
用与底面成45°角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.3柱面与平面的截面练习卷(解析版) 题型:选择题
某舞台灯光设计师为了在地板上设计图案,他把一端向下发光的光源和支架之间的角度固定为θ角,支架的一端固定在地板的中心位置,支架的另一端固定在天花板的适当位置,当光源围绕支架以θ角快速旋转时,地板上可能出现的图案有( )
A.椭圆 B.抛物线 C.圆 D.以上均有可能
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:选择题
(2009•奉贤区二模)已知一球半径为2,球面上A、B两点的球面距离为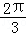 ,则线段AB的长度为( )
,则线段AB的长度为( )
A.1 B. C.2 D.2
C.2 D.2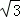
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
(2012•杭州一模)已知函数f(x)= ,要得到
,要得到 f′(x)的图象,只需将f(x)的图象( )个单位.
f′(x)的图象,只需将f(x)的图象( )个单位.
A.向右平移 B.向左平移
B.向左平移 C.向右平移
C.向右平移 D.向左平移
D.向左平移
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com