
分析 由函数f(x)的定义域为[-2,2],可得f(2x)的定义域为满足-2≤2x≤2的x的取值集合,再与2x+1>0的解集取交集即可得到函数y=f(2x)•ln(2x+1)的定义域.
解答 解:要使原函数有意义,则$\left\{{\begin{array}{l}{-2≤2x≤2}\\{2x+1>0}\end{array}}\right.$,解得$-\frac{1}{2}<x≤1$.
∴函数y=f(2x)•ln(2x+1)的定义域为$(-\frac{1}{2},1]$.
故答案为:$(-\frac{1}{2},1]$.
点评 本题考查函数的定义域及其求法,考查了不等式组的解法,是基础题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD,底面ABCD是∠ABC=60°的菱形,侧面PAD是边长为2的正三角形,且与底面ABCD垂直,M为PC的中点.
如图,四棱锥P-ABCD,底面ABCD是∠ABC=60°的菱形,侧面PAD是边长为2的正三角形,且与底面ABCD垂直,M为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四边形ABCD中,CB=CA=$\frac{1}{2}$AD=1,$\overrightarrow{CA}•\overrightarrow{AD}$=-1,sin∠BCD=$\frac{3}{5}$.
如图,在四边形ABCD中,CB=CA=$\frac{1}{2}$AD=1,$\overrightarrow{CA}•\overrightarrow{AD}$=-1,sin∠BCD=$\frac{3}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<1} | B. | {x|1≤x≤2} | C. | {x|-1≤x<1} | D. | {x|1≤x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [1,+∞) | C. | (0,1] | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
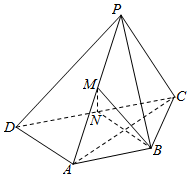 如图,在四棱锥P-ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点.
如图,在四棱锥P-ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | [-1,0) | C. | [-2,-1] | D. | [-2,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com