
分析 (1)由和差角公式化简可得f(x)=sin(2x+$\frac{π}{6}$),易得最小正周期和递减区间;
(2)由图象变换的规则,逐步变换可得;
(3)作出函数y=x和g(x)的图象,数形结合可得.
解答 解:(1)化简可得f(x)=cos2x+$\sqrt{3}$sinxcosx-$\frac{1}{2}$
=$\frac{\sqrt{3}}{2}$•2sinxcosx+$\frac{1}{2}$(2cos2x-1)
=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x
=sin(2x+$\frac{π}{6}$),
∴f(x)最小正周期T=$\frac{2π}{2}$=π,
由2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$可解得kπ+$\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$,
∴函数f(x)的递减区间为[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$](k∈Z);
(2)由图象变换可得y=sin(2x+$\frac{π}{6}$)向右平移$\frac{π}{12}$个单位得到y=sin[2(x-$\frac{π}{12}$)+$\frac{π}{6}$]=sin2x,
再横坐标伸长到原来的两倍得到y=sinx,然后纵坐标缩为原来的m倍得到y=msinx,
再向上平移一个单位得到g(x)=msinx+1;
(3)作出函数y=x和g(x)=msinx+1,(0<m<$\frac{1}{2}$)的图象,
可得g(x)=x实根个数为1
点评 本题考查两角和与差的三角函数公式,涉及三角函数的周期性和单调性以及图象变换,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{6}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
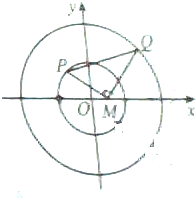 如图,已知圆E1:x2+y2=4,E2:x2+y2=16,点M(1,0),动点P,Q分别在圆E1,E2上,且MP⊥MQ.
如图,已知圆E1:x2+y2=4,E2:x2+y2=16,点M(1,0),动点P,Q分别在圆E1,E2上,且MP⊥MQ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com