
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | $\frac{1}{6}$ |
分析 设|AF|=a,|BF|=b,连接AF、BF.由抛物线定义得2|MN|=a+b,由余弦定理可得|AB|2=(a+b)2-3ab,进而根据基本不等式,求得|AB|的取值范围,从而得到本题答案.
解答 解:设|AF|=a,|BF|=b,连接AF、BF,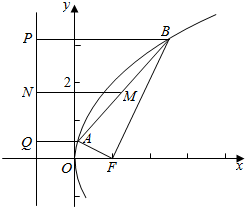
由抛物线定义,得|AF|=|AQ|,|BF|=|BP|,
在梯形ABPQ中,2|MN|=|AQ|+|BP|=a+b.
由余弦定理得,
|AB|2=a2+b2-2abcos60°=a2+b2-ab,
配方得,|AB|2=(a+b)2-3ab,
又∵ab≤($\frac{a+b}{2}$)2,
∴(a+b)2-3ab≥(a+b)2-$\frac{3}{4}$(a+b)2=$\frac{1}{4}$(a+b)2
得到|AB|≥$\frac{1}{2}$(a+b).
∴$\frac{|MN|}{|AB|}$≤1,
即$\frac{|MN|}{|AB|}$的最大值为1.
故选:B.
点评 本题给出抛物线的弦AB对焦点F所张的角为直角,求AB中点M到准线的距离与AB比值的取值范围,着重考查了抛物线的定义与简单几何性质、梯形的中位线定理和基本不等式求最值等知识,属于中档题.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
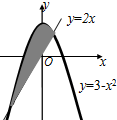
| A. | 10 | B. | $\frac{31}{3}$ | C. | 11 | D. | $\frac{32}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 小明 | 6 | 6 | 9 | 9 |
| 小红 | 7 | 9 | 6 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com