
分析 (1)先求出直线l在两坐标轴上的截距,再利用 l在两坐标轴上的截距相等 建立方程,解方程求出a的值,从而得到所求的直线l方程.
(2)把直线l的方程可化为 y=-(a+1)x+a-2,由题意得$\left\{\begin{array}{l}{-(a+1)≥0}\\{a-2≤0}\end{array}\right.$,解不等式组求得a的范围.
(3)通过变量分离法得到两条相关的曲线方程,联列方程组得到定点坐标.
解答 解:(1)令x=0,得y=a-2.
令y=0,得x=$\frac{a-2}{a+1}$(a≠-1).
∵l在两坐标轴上的截距相等,
∴a-2=$\frac{a-2}{a+1}$,解之,得a=2或a=0.
∴所求的直线l方程为3x+y=0或x+y+2=0.
(2)直线l的方程可化为 y=-(a+1)x+a-2.
∵l不过第二象限,
∴$\left\{\begin{array}{l}{-(a+1)≥0}\\{a-2≤0}\end{array}\right.$,
∴a≤-1.
∴a的取值范围为(-∞,-1].
(3)∵(a+1)x+y-2-a=0(a∈R),
∴a(x-1)+(x+y-2)=0.
令$\left\{\begin{array}{l}{x-1=0}\\{x+y-2=0}\end{array}\right.$,
得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
∴直线l:(a+1)x+y+2-a=0(a∈R)必过定点(1,-3).
点评 本题考查直线在坐标轴上的截距的定义,用待定系数法求直线的方程,以及确定直线位置的几何要素.直线过定点问题,可以用参变量分离法,还可以用特殊值代入法.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2)(3) | B. | (1)(3)(4) | C. | (2)(3)(5) | D. | (3)(4)(5) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | b | 50 |
| 乙班 | c | d | 50 |
| 合计 | 70 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
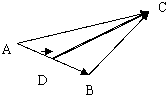 具有方向的线段叫做有向线段(向量),以A为起点,B为终点的有向线段记作$\overrightarrow{AB}$,已知$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$,如图所示:如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{AC}$=$\overrightarrow{a}$+$\overrightarrow{b}$.若D为AB的中点,$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$,若BE为AC上的中线,则用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{DC}$为$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.
具有方向的线段叫做有向线段(向量),以A为起点,B为终点的有向线段记作$\overrightarrow{AB}$,已知$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$,如图所示:如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{AC}$=$\overrightarrow{a}$+$\overrightarrow{b}$.若D为AB的中点,$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$,若BE为AC上的中线,则用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{DC}$为$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com